Crypto
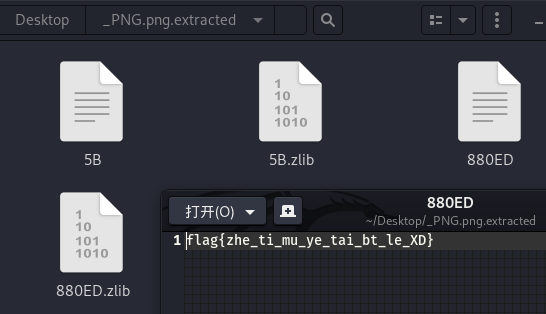
base_family
R1JDRE9PSlVHTTJUSU5CV0c1QkRNTVJUR1EzVEdOUlZHVkRER01KWEdNMlVNTlJXRzQyVE1SSlhJUT09PT09PQ==使用basecrack工具爆破即可
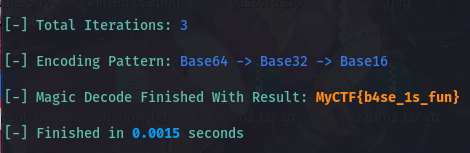
sign_of_rsa
sign_of_rsa.py
from gmpy2 import *
from Crypto.Util.number import bytes_to_long
from secret import flag
p = getPrime(256)
q = getPrime(256)
n = p*q
e = 65537
c = pow(bytes_to_long(flag),e,n)
print(n)
print(c)
#results
'''
n = 39850348348140357386937824592821246833650548134289278936384136986131545685673
c = 22654877589152446246623200249483354618377874659789586340291352819969094640373
'''基本的RSA加密,由于n长度较小,可以直接使用在线网站分解
解密脚本如下
from Crypto.Util.number import *
import gmpy2
e = 65537
p = 195718419798538086931252543197938665739
q = 203610617688208099919841873282692804507
c = 22654877589152446246623200249483354618377874659789586340291352819969094640373
n = 39850348348140357386937824592821246833650548134289278936384136986131545685673
phi = (p-1)*(q-1)
d=gmpy2.invert(e,phi)
print(long_to_bytes(pow(c,d,n)))dangerous_rsa
附件 dangerous.txt
n = 14260179413452225026626520413415913481947815280801452969658040900725734766818110442573419765439527829601658184611857860832652310715944637802697197369992026898178496171713366708106657107697251079040116819805796572460332676649583314077053585466751585984550070799033582063390018655490838759562591042086818078114758940171334609281034283533387120610269318426605948424207612580788200503206417837155761224407072204676978954436370188052696874682133870118172384079547713639614066941148301873701044940561882434831078356129049722022003275742800204214005563245366826778265174726035421839087923692022079608889315875963737773026537
e = 3
c = 469541014837708504765973500537960637072461753248685866039651501322343570189154590100339697910290787883976473556732111567690396987367251269184489582194054713945124159391510206287493803477304026899976395279229849456218990448361778580604696260932623061861可以发现e很小,可以使用低加密指数攻击,原理如下
倘若有$m^3 \equiv c\mod n$,我们可以计算出$c\mod n \equiv x$,于是$m^3$可以表示为$m^3=k*n+x$。
于是可以得到$m=(k*n+x)^\frac 13$。此时$n$、$x$都是已知的,我们只需要爆破$k$即可,脚本如下
from Crypto.Util.number import *
import gmpy2
n = 14260179413452225026626520413415913481947815280801452969658040900725734766818110442573419765439527829601658184611857860832652310715944637802697197369992026898178496171713366708106657107697251079040116819805796572460332676649583314077053585466751585984550070799033582063390018655490838759562591042086818078114758940171334609281034283533387120610269318426605948424207612580788200503206417837155761224407072204676978954436370188052696874682133870118172384079547713639614066941148301873701044940561882434831078356129049722022003275742800204214005563245366826778265174726035421839087923692022079608889315875963737773026537
e = 3
c = 469541014837708504765973500537960637072461753248685866039651501322343570189154590100339697910290787883976473556732111567690396987367251269184489582194054713945124159391510206287493803477304026899976395279229849456218990448361778580604696260932623061861
for k in range(100000):
m=gmpy2.iroot((k*n+c),3)
if m[1]:
print(long_to_bytes(int(m[0])))ezVigenère
附件如下 ezVigenere.txt
Tig Vjieogrf eiqjes ks b oeujoe qf fpcsapuknh clqjacgtje tfzt ca utknh c sftifu og knugrxqvfp Cbgsbt cjrhfts, ccsff oo vhf neuvesu og c kfawptd. Jv enrlpas b hoso og romaamrhbdeukc twbtviuwtjqn.
Gkrtv dfucskbff bz Iipxao Dauvitva Cglmcsp kn 1553, uje dkpigr ju ebuy uq uofesutbpd bpd jopmgmfpt, cwt jv rfuitvee clm ctugmqvs uq bsgal kt vptjn 1863, titef eeovusket naugr. Ujit gaspee kt uje egsdtiqvipp lf ehjhfscgf knegcikfgtacne (Gteoeh gqr 'uje jpdfeiqjescbmg cjrhft'). Mbpy qgoqne icvf vrjgd uq inrlfoeov eoerzrtjqn tehfoet vhbv asg etueovibnlz Xihgnfte dkpigrt. Kn 1863, Gtiffrjeh Lcsjukj yat vhf hisut uq pvdljuh b ieogrbn mfvhpf og fedkpigrjpg Wkgfpesg cjrhfts. Jp tig 19ti eeovusa tig sdjeng wbu mjuauvrjduugd uq Bmcitg df Xihgnfte, bpd tq adsujtee ktt rrfueov nboe.NaCUH{iovesgsu1pg_Wkgfpesg}提示是维吉尼亚密码,直接使用在线网站爆破即可,语言选择English。解密如下
The Vigenere cipher is a method of encrypting alphabetic text by using a series of interwoven Caesar ciphers, based on the letters of a keyword. It employs a form of polyalphabetic substitution.
First described by Giovan Battista Bellaso in 1553, the cipher is easy to understand and implement, but it resisted all attempts to break it until 1863, three centuries later. This earned it the description le chiffrage indechiffrable (French for 'the indecipherable cipher'). Many people have tried to implement encryption schemes that are essentially Vigenere ciphers. In 1863, Friedrich Kasiski was the first to publish a general method of deciphering Vigenere ciphers. In the 19th century the scheme was misattributed to Blaise de Vigenere, and so acquired its present name.MyCTF{interest1ng_Vigenere}small_e_rsa
附件如下
n = 22612558766336617211840599448975974745256849245806865510254887775303220464436296743202104281087830846737553391522672779595262447637518193629900803759161068321285528992940424408118993846851198354683869707130581738909562933774213378368642990373151379410885726600630804276961376758392915770882894715210924142966575189669626093078070697241456585571609865004187853405054215757097306563637796157890114569877083265075672919618795563071943399272418193784317011039311665127016102442672159202973936737227797281501028747748451124895212529467337124277406141501950580988988770182388517493500314712091121641895008217769215494990441
e = 3
c = 10011780130910405446639483087148914825890567341153314814800075710617423104196656645588697433463773762094145308451961442623594155715848886950657916268596009123190696051963503335767054894409719194307635827084651490862827346134351185912243941624861461491141144055281035700685193183811841853003510066616123528887684322912838564303796650992814423396466611666746530669371675103869575628017500774712951998427498621387659193853092993834803310282777907343553646320596054723456810301788301473878364486194171337758656092261411020434555946551844273796140784593239561640881510064657685745893876157893534071528670545904909115875399和前一题一样,低指数加密攻击,直接上脚本
from Crypto.Util.number import *
import gmpy2
n = 22612558766336617211840599448975974745256849245806865510254887775303220464436296743202104281087830846737553391522672779595262447637518193629900803759161068321285528992940424408118993846851198354683869707130581738909562933774213378368642990373151379410885726600630804276961376758392915770882894715210924142966575189669626093078070697241456585571609865004187853405054215757097306563637796157890114569877083265075672919618795563071943399272418193784317011039311665127016102442672159202973936737227797281501028747748451124895212529467337124277406141501950580988988770182388517493500314712091121641895008217769215494990441
e = 3
c = 10011780130910405446639483087148914825890567341153314814800075710617423104196656645588697433463773762094145308451961442623594155715848886950657916268596009123190696051963503335767054894409719194307635827084651490862827346134351185912243941624861461491141144055281035700685193183811841853003510066616123528887684322912838564303796650992814423396466611666746530669371675103869575628017500774712951998427498621387659193853092993834803310282777907343553646320596054723456810301788301473878364486194171337758656092261411020434555946551844273796140784593239561640881510064657685745893876157893534071528670545904909115875399
for k in range(100000):
m=gmpy2.iroot((k*n+c),3)
if m[1]:
print(long_to_bytes(int(m[0])))MyFunction
附件如下
#MyFunction.py
from math import log
from secret import flag
def f(x):
return x*log(x) #log(x) is "y=ln(x)" used in maths
for i in flag:
print(f(ord(i)))
#output.txt部分数据
185.81764852357878
574.4990091338454
……
……
334.47301748273367
205.46467336623422
220.40332518778592
483.0166535107027
545.6671947617738
603.5392171627877flag的每一位的ascii值是通过f()函数加密的。虽然我们无法直接通过加密数据求出对应的字符,但是由于ascii码的个数有限,我们可以求出所有ascii码加密后的结果,再与output数据比对便可得到相应的字符。脚本如下
import math
def d(n):
for i in range(1,127):
if i*math.log(i)==n:
return i
def flag(file):
with open(file,'r') as f:
rflag=f.readlines()
for i in range(len(rflag)):
rflag[i]=chr(d(float(rflag[i].replace(r'\n',''))))
return ''.join(rflag)
print(flag("output.txt"))BlackGiveRSA
附件如下
from Crypto.Util.number import *
from secret import flag,p,q
assert q>p
n=p*q
e=10007
assert len(flag)==42
for i in range(6):
m=bytes_to_long(flag[i*7:i*7+7])
print(pow(m,e,n))
print("Encryption using modulus n=",n)
"""
OutPut:
1150947306854980854
243703926267532432
1069319314811079682
688582941857504686
670683629344243145
1195068175327355214
Encryption using modulus n= 1687126110378632809
"""白给题,只是把flag拆分了,脚本如下
from Crypto.Util.number import *
import gmpy2
p=1175078221
q=1435756429
n=p*q
phi=(p-1)*(q-1)
e=10007
d=gmpy2.invert(e,phi)
flag=[1150947306854980854,
243703926267532432,
1069319314811079682,
688582941857504686,
670683629344243145,
1195068175327355214]
FLAG=b''
for i in flag:
flag0=long_to_bytes(gmpy2.powmod(i,d,n))
FLAG+=flag0
print(FLAG)ezECC
附件如下 EzECC.sage
#Alice do this
p=14050339
a=1
b=3243167
E = EllipticCurve(GF(p),[a,b])
G=E(7112688,7410262)
k=random.randrange(1,G.order())
K=k*G
print(K)
#(6562993 : 2753874 : 1)
######################################
######################################
#Bob do this
import random
flag="0xGame{xxxxxxxx}"
table='abcdefghijklmnopqrstuvwxyz'
m=flag[7:-1]
m1=m[:4]
m2=m[4:]
m_1=''
m_2=''
for i in m1:
s=str(table.index(i)+1)
if len(s)<2:
s='0'+s
m_1+=s
for i in m2:
s=str(table.index(i)+1)
if len(s)<2:
s='0'+s
m_2+=s
x=int(m_1)
y=int(m_2)
P=E(x,y)
r=random.randrange(1,G.order())
C1=P+r*K
C2=r*G
print(C1)
#(3095063 : 1465594 : 1)
print(C2)
#(6437074 : 4385056 : 1)
######################################
######################################
#Eva wants to know the flag.
#Can you help Eva?我们先来分析一下Alice和Eva分别做了什么
对于Alice
在有限域$GF(14050339)$上生成椭圆曲线$Ep(1, 3243167)$,然后选取$G=E(7112688,7410262)$作为基点。选取随机数$k$作为私钥,计算公钥$K=kG=E(6562993,2753874)$。最后将$K$、$k$、$Ep$发送给Eva。
对于Eva
使用算法将明文$m$镶嵌到椭圆曲线$Ep$上,得到点$P$,计算密文$C_1=P+r*K$以及$C_2=r*G$。
对于以上过程,我们可以使用Pohlig-Hellman方法进行攻击。
sage脚本如下
#分解G的阶
sage: p=14050339
....: a=1
....: b=3243167
....: E = EllipticCurve(GF(p),[a,b])
....: G=E(7112688,7410262)
....: K=E(6562993,2753874)
....: factor(G.order())
....:
2 * 3 * 1170811
#求离散对数li
factors=[2,3,1170811]
sage: result=[]
sage: for fac in factors:
....: t=int(G.order())/int(fac)
....: res=discrete_log(t*K,t*Q,operation="+")
....: result+=[res]
....: print("factor:"+str(fac)+",Discrete Log"+str(res))
....:
factor:2,Discrete Log1
factor:3,Discrete Log1
factor:1170811,Discrete Log770032
#求k
sage: logs=[1,1,770032]
....: crt(logs,factors)
4282465
#求P
sage: C1=E(3095063,1465594)
sage: C2=E(6437074,4385056)
sage: C1-k*C2
(12050118 : 14050303 : 1)求出明文$P(12050118,14050303)$后,求Eva逆加密即可,Python脚本如下
table='abcdefghijklmnopqrstuvwxyz'
a=(12050118 ,14050303)
def flag(a):
flag=""
x=a[0]
y=a[1]
m=str(x)+str(y)
for i in range(0,16,2):
flag+=str(table[int(m[i:i+2])-1])
return flag
print("0xGame{"+flag(a)+"}")CryptoSignin
附件如下
在RSA加密中:
已知:
n=2422711508900009723470102727278184898228579351729629175495904760516536114771819178772843940622693480942295987032442940867670858858530606887743557817380121361626756206355705110299827107648704348792184242506797212331641569408152865458082131811787893384573565771304686373397987779236692592582009393836324438173880350455958049987506807351970912049246353746635267159741115761548052126938491673479606393396100458729618059852813438444299361468512008386975558106274324688665963516424534366163011821633197140729560513838981241752422348968312410911097523311183305812013220724215584901550592570168096761576532621840320623463208702401829189862290303098674021012353400081288819532365151476738751064469957971192132666136590103567843662591585345483671185892760751481722342403025068374371716176981888876927119331602694699049322860285991375002326127401769287658952682585275891296760732815680898653162425658904911584903825163141576325803464119867837508173795728753701563149748508464162635777787788266240105654089919642728171076155284842273517797069725130328742992830894075552022372717019366081516680737
e=10007
c=1285901843278876234855607310979623200548989981628646673003523113580651626686523566799395153922258813222744927018205882436414589516795415393990321785993777190284046937462277341231780571523062023964463963139910673601962881978696384360480028132774373962893042697866284303407898274683337284548529324550392212212259945699167254341062208031468355814520907121576009140399280898693924706067921614961798886587174234822238887374399666546113213239071736098162263227821798099750616137755055435397986788792824117529508255014392344357337010003489080209442530630893119917536518243474797351694663533728052713570044084663268350004738561234330890283895430742958255842196396542672482459665354739161276178850775803757753274712331067038077233072381051447436014423088822190073982228377699578821863871042501139434131053044240618505423456248872825597521393564957261041606004454706987978944644129728005540587982321571481413548381251589071459468890948819121023006292105804319208332473499823959882524985324120811768843639294924500467781666073366713198751960913508720530656411097981933156605831180926219778514434
求5*m加密后的结果(c是m的加密结果),由于数字比较长,只需要将5*m的加密结果(十进制格式)的最后25位数包上MyCTF{}提交即可。若不足25位需要在前面补0到25位。最后25位如果是0开头也要保留0已知$m^e \equiv c \mod n$。计算$(5*m)^e \equiv x \mod n$,可得$5^e*m^e \equiv c*5^e \mod n$。$x \equiv c*5^e \mod n$,计算脚本如下
import gmpy2
n=2422711508900009723470102727278184898228579351729629175495904760516536114771819178772843940622693480942295987032442940867670858858530606887743557817380121361626756206355705110299827107648704348792184242506797212331641569408152865458082131811787893384573565771304686373397987779236692592582009393836324438173880350455958049987506807351970912049246353746635267159741115761548052126938491673479606393396100458729618059852813438444299361468512008386975558106274324688665963516424534366163011821633197140729560513838981241752422348968312410911097523311183305812013220724215584901550592570168096761576532621840320623463208702401829189862290303098674021012353400081288819532365151476738751064469957971192132666136590103567843662591585345483671185892760751481722342403025068374371716176981888876927119331602694699049322860285991375002326127401769287658952682585275891296760732815680898653162425658904911584903825163141576325803464119867837508173795728753701563149748508464162635777787788266240105654089919642728171076155284842273517797069725130328742992830894075552022372717019366081516680737
e=10007
c=1285901843278876234855607310979623200548989981628646673003523113580651626686523566799395153922258813222744927018205882436414589516795415393990321785993777190284046937462277341231780571523062023964463963139910673601962881978696384360480028132774373962893042697866284303407898274683337284548529324550392212212259945699167254341062208031468355814520907121576009140399280898693924706067921614961798886587174234822238887374399666546113213239071736098162263227821798099750616137755055435397986788792824117529508255014392344357337010003489080209442530630893119917536518243474797351694663533728052713570044084663268350004738561234330890283895430742958255842196396542672482459665354739161276178850775803757753274712331067038077233072381051447436014423088822190073982228377699578821863871042501139434131053044240618505423456248872825597521393564957261041606004454706987978944644129728005540587982321571481413548381251589071459468890948819121023006292105804319208332473499823959882524985324120811768843639294924500467781666073366713198751960913508720530656411097981933156605831180926219778514434
print("MyCTF{"+str((gmpy2.powmod(5,e,n)*c)%n)[-25:]+"}")equation
附件如下
n = 32366272889292879088882195998253721958216118427319043123590736165426820884306499 72505072774953729579662378169088625526801609681954247481445743753234195846484864 32006599163876925633672709233622634624856268632786346986362195709956131636378579 62196938268241034329466928075048970301826587646917598116612437415879221437295531 62851338441425836836991694674238970335517972711258059268343941626154786549172502 55862486052722915840287749675536279427245796323892544964098492168414096046869805 57654983994405692268823696566554514932549687234389560838939048535333918846662927 37458538676672383829067193778907330696675919164932574607371728825246281795273459 76928309946222556355469080585815244775185325189241129765631970101922519297464453 12969880127879576958492529042343256141675368594461418257288354657105617752796615 735654975200326101463143024542800708390095145361
e = 906371
c = 15326438748659000169738486078886997781541935909035823368289334280968233481809714 57442806487923782791476074043839608581840010075291847465785855438877172406438370 13958976180452762813988244342748485576539090899942444359727106323366393353000236 67869547648881808002952139588112935030846125601449819192271492110196773991802015 58097853266319970695091034307000836897969305299098522785271966824556923885790865 52273856824143198463214294288100229095300504441058372106016149332214176629867255 39709495237298445020038006845869543594704774018595363714269915863872404761678621 06624438722044927035548292437401481179012575168951192364641026966545994140064500 76556965322449866045219494771596497487547608749197439023078241981268930024864452 62315126416725774433901321311453440889692050265638750239216391568288836776466397 695369910655394827082589725264284100323144743368
f = 4071 * p + 7840 * q =
70609572383507708646716591625555712379946460153989879089689539734922903656784859 76461877105488188285509721736325291122948521094751427059364999919801842759573386 84972088214573159137781785322672174195875565196400090478547076497516635140170946 26487619210733938544175505589938842947647526503757953723232894419183885106501307 58779288877040691361960692685141215708440168846913057117411471730595050109728244 6764439401475500746719477183已知$n=p*q$以及$f=4071*p+7840*q$,联立以上两式可以解出$p$,$q$。脚本如下
from Crypto.Util.number import *
import gmpy2
import sympy
n = 32366272889292879088882195998253721958216118427319043123590736165426820884306499725050727749537295796623781690886255268016096819542474814457437532341958464848643200659916387692563367270923362263462485626863278634698636219570995613163637857962196938268241034329466928075048970301826587646917598116612437415879221437295531628513384414258368369916946742389703355179727112580592683439416261547865491725025586248605272291584028774967553627942724579632389254496409849216841409604686980557654983994405692268823696566554514932549687234389560838939048535333918846662927374585386766723838290671937789073306966759191649325746073717288252462817952734597692830994622255635546908058581524477518532518924112976563197010192251929746445312969880127879576958492529042343256141675368594461418257288354657105617752796615735654975200326101463143024542800708390095145361
e = 906371
c = 15326438748659000169738486078886997781541935909035823368289334280968233481809714574428064879237827914760740438396085818400100752918474657858554388771724064383701395897618045276281398824434274848557653909089994244435972710632336639335300023667869547648881808002952139588112935030846125601449819192271492110196773991802015580978532663199706950910343070008368979693052990985227852719668245569238857908655227385682414319846321429428810022909530050444105837210601614933221417662986725539709495237298445020038006845869543594704774018595363714269915863872404761678621066244387220449270355482924374014811790125751689511923646410269665459941400645007655696532244986604521949477159649748754760874919743902307824198126893002486445262315126416725774433901321311453440889692050265638750239216391568288836776466397695369910655394827082589725264284100323144743368
f=70609572383507708646716591625555712379946460153989879089689539734922903656784859764618771054881882855097217363252911229485210947514270593649999198018427595733868497208821457315913778178532267217419587556519640009047854707649751663514017094626487619210733938544175505589938842947647526503757953723232894419183885106501307587792888770406913619606926851412157084401688469130571174114717305950501097282446764439401475500746719477183
# p,q(21407,21408)
p=sympy.Symbol('p')
q=sympy.Symbol('q')
fx = 4071 * p + 7840 * q-70609572383507708646716591625555712379946460153989879089689539734922903656784859764618771054881882855097217363252911229485210947514270593649999198018427595733868497208821457315913778178532267217419587556519640009047854707649751663514017094626487619210733938544175505589938842947647526503757953723232894419183885106501307587792888770406913619606926851412157084401688469130571174114717305950501097282446764439401475500746719477183
fy=p*q-32366272889292879088882195998253721958216118427319043123590736165426820884306499725050727749537295796623781690886255268016096819542474814457437532341958464848643200659916387692563367270923362263462485626863278634698636219570995613163637857962196938268241034329466928075048970301826587646917598116612437415879221437295531628513384414258368369916946742389703355179727112580592683439416261547865491725025586248605272291584028774967553627942724579632389254496409849216841409604686980557654983994405692268823696566554514932549687234389560838939048535333918846662927374585386766723838290671937789073306966759191649325746073717288252462817952734597692830994622255635546908058581524477518532518924112976563197010192251929746445312969880127879576958492529042343256141675368594461418257288354657105617752796615735654975200326101463143024542800708390095145361
pq=sympy.solve([fx,fy])[0]
p=int(pq[p])
q=int(pq[q])
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
print(long_to_bytes(pow(c,d,n)))hardrsa
原题,附件如下
from Crypto.Util.number import *
import gmpy2
p = getPrime(512)
q = getPrime(512)
n = p**4*q
e = 65537
phi = gmpy2.lcm(p - 1, q - 1)
d = gmpy2.invert(e, phi)
dp = d % (p - 1)
m = bytes_to_long(flag)
c = pow(m, e, n)
x = 2019*p**2 + 2020*p**3 + 2021*p**4
c1 = pow(g, x, y)
print ("dp = " + str(dp))
print( "c1 = " + str(c1))
#y = 449703347709287328982446812318870158230369688625894307953604074502413258045265502496365998383562119915565080518077360839705004058211784369656486678307007348691991136610142919372779782779111507129101110674559235388392082113417306002050124215904803026894400155194275424834577942500150410440057660679460918645357376095613079720172148302097893734034788458122333816759162605888879531594217661921547293164281934920669935417080156833072528358511807757748554348615957977663784762124746554638152693469580761002437793837094101338408017407251986116589240523625340964025531357446706263871843489143068620501020284421781243879675292060268876353250854369189182926055204229002568224846436918153245720514450234433170717311083868591477186061896282790880850797471658321324127334704438430354844770131980049668516350774939625369909869906362174015628078258039638111064842324979997867746404806457329528690722757322373158670827203350590809390932986616805533168714686834174965211242863201076482127152571774960580915318022303418111346406295217571564155573765371519749325922145875128395909112254242027512400564855444101325427710643212690768272048881411988830011985059218048684311349415764441760364762942692722834850287985399559042457470942580456516395188637916303814055777357738894264037988945951468416861647204658893837753361851667573185920779272635885127149348845064478121843462789367112698673780005436144393573832498203659056909233757206537514290993810628872250841862059672570704733990716282248839
#g = 2
#dp = 379476973158146550831004952747643994439940435656483772269013081580532539640189020020958796514224150837680366977747272291881285391919167077726836326564473
#c = 57248258945927387673579467348106118747034381190703777861409527336272914559699490353325906672956273559867941402281438670652710909532261303394045079629146156340801932254839021574139943933451924062888426726353230757284582863993227592703323133265180414382062132580526658205716218046366247653881764658891315592607194355733209493239611216193118424602510964102026998674323685134796018596817393268106583737153516632969041693280725297929277751136040546830230533898514659714717213371619853137272515967067008805521051613107141555788516894223654851277785393355178114230929014037436770678131148140398384394716456450269539065009396311996040422853740049508500540281488171285233445744799680022307180452210793913614131646875949698079917313572873073033804639877699884489290120302696697425
#c1 = 78100131461872285613426244322737502147219485108799130975202429638042859488136933783498210914335741940761656137516033926418975363734194661031678516857040723532055448695928820624094400481464950181126638456234669814982411270985650209245687765595483738876975572521276963149542659187680075917322308512163904423297381635532771690434016589132876171283596320435623376283425228536157726781524870348614983116408815088257609788517986810622505961538812889953185684256469540369809863103948326444090715161351198229163190130903661874631020304481842715086104243998808382859633753938512915886223513449238733721777977175430329717970940440862059204518224126792822912141479260791232312544748301412636222498841676742208390622353022668320809201312724936862167350709823581870722831329406359010293121019764160016316259432749291142448874259446854582307626758650151607770478334719317941727680935243820313144829826081955539778570565232935463201135110049861204432285060029237229518297291679114165265808862862827211193711159152992427133176177796045981572758903474465179346029811563765283254777813433339892058322013228964103304946743888213068397672540863260883314665492088793554775674610994639537263588276076992907735153702002001005383321442974097626786699895993544581572457476437853778794888945238622869401634353220344790419326516836146140706852577748364903349138246106379954647002557091131475669295997196484548199507335421499556985949139162639560622973283109342746186994609598854386966520638338999059题目可以分为两部分,首先第一部分我们求$p$。
求$p$
由题目可知$x=2019*p^2 + 2020*p^3 + 2021*p^4$,要求$p$,我们首先要求出$x$。而$g^x \equiv c_1 \mod y$,求$x$即为离散对数问题,但由于底数$g$较小,所以容易求出$x$。可以使用sympy包下的discrete_log()函数来求解,脚本如下
import sympy
y=449703347709287328982446812318870158230369688625894307953604074502413258045265502496365998383562119915565080518077360839705004058211784369656486678307007348691991136610142919372779782779111507129101110674559235388392082113417306002050124215904803026894400155194275424834577942500150410440057660679460918645357376095613079720172148302097893734034788458122333816759162605888879531594217661921547293164281934920669935417080156833072528358511807757748554348615957977663784762124746554638152693469580761002437793837094101338408017407251986116589240523625340964025531357446706263871843489143068620501020284421781243879675292060268876353250854369189182926055204229002568224846436918153245720514450234433170717311083868591477186061896282790880850797471658321324127334704438430354844770131980049668516350774939625369909869906362174015628078258039638111064842324979997867746404806457329528690722757322373158670827203350590809390932986616805533168714686834174965211242863201076482127152571774960580915318022303418111346406295217571564155573765371519749325922145875128395909112254242027512400564855444101325427710643212690768272048881411988830011985059218048684311349415764441760364762942692722834850287985399559042457470942580456516395188637916303814055777357738894264037988945951468416861647204658893837753361851667573185920779272635885127149348845064478121843462789367112698673780005436144393573832498203659056909233757206537514290993810628872250841862059672570704733990716282248839
g = 2
c1=78100131461872285613426244322737502147219485108799130975202429638042859488136933783498210914335741940761656137516033926418975363734194661031678516857040723532055448695928820624094400481464950181126638456234669814982411270985650209245687765595483738876975572521276963149542659187680075917322308512163904423297381635532771690434016589132876171283596320435623376283425228536157726781524870348614983116408815088257609788517986810622505961538812889953185684256469540369809863103948326444090715161351198229163190130903661874631020304481842715086104243998808382859633753938512915886223513449238733721777977175430329717970940440862059204518224126792822912141479260791232312544748301412636222498841676742208390622353022668320809201312724936862167350709823581870722831329406359010293121019764160016316259432749291142448874259446854582307626758650151607770478334719317941727680935243820313144829826081955539778570565232935463201135110049861204432285060029237229518297291679114165265808862862827211193711159152992427133176177796045981572758903474465179346029811563765283254777813433339892058322013228964103304946743888213068397672540863260883314665492088793554775674610994639537263588276076992907735153702002001005383321442974097626786699895993544581572457476437853778794888945238622869401634353220344790419326516836146140706852577748364903349138246106379954647002557091131475669295997196484548199507335421499556985949139162639560622973283109342746186994609598854386966520638338999059
x=sympy.discrete_log(y,c1,g)
print(x)
#x=43776275628859890575232443794319298551934804213472744927022818696759188901977390266973172755658396197421139420206549889337117978597883154859965236605452518446448639813055134133587564045471804447818058571586426895800984805588363855865218690877547419152765512143095217413477343835473963637692441032136163289964756172316289469159500312630529091350636808491697553069388388303341623047737553556123142002737059936569931163197364571478509576816349348146215101250803826590694039096063858424405382950769415272111843039715632655831594224288099608827345377164375927559338153505991404973888594356664393487249819589915881178770048740解出$x$的值之后,由于$p$的值为方程$x=2019*p^2 + 2020*p^3 + 2021*p^4$的根,可以使用sage解方程求$p$,脚本如下
y=449703347709287328982446812318870158230369688625894307953604074502413258045265502496365998383562119915565080518077360839705004058211784369656486678307007348691991136610142919372779782779111507129101110674559235388392082113417306002050124215904803026894400155194275424834577942500150410440057660679460918645357376095613079720172148302097893734034788458122333816759162605888879531594217661921547293164281934920669935417080156833072528358511807757748554348615957977663784762124746554638152693469580761002437793837094101338408017407251986116589240523625340964025531357446706263871843489143068620501020284421781243879675292060268876353250854369189182926055204229002568224846436918153245720514450234433170717311083868591477186061896282790880850797471658321324127334704438430354844770131980049668516350774939625369909869906362174015628078258039638111064842324979997867746404806457329528690722757322373158670827203350590809390932986616805533168714686834174965211242863201076482127152571774960580915318022303418111346406295217571564155573765371519749325922145875128395909112254242027512400564855444101325427710643212690768272048881411988830011985059218048684311349415764441760364762942692722834850287985399559042457470942580456516395188637916303814055777357738894264037988945951468416861647204658893837753361851667573185920779272635885127149348845064478121843462789367112698673780005436144393573832498203659056909233757206537514290993810628872250841862059672570704733990716282248839
num=43776275628859890575232443794319298551934804213472744927022818696759188901977390266973172755658396197421139420206549889337117978597883154859965236605452518446448639813055134133587564045471804447818058571586426895800984805588363855865218690877547419152765512143095217413477343835473963637692441032136163289964756172316289469159500312630529091350636808491697553069388388303341623047737553556123142002737059936569931163197364571478509576816349348146215101250803826590694039096063858424405382950769415272111843039715632655831594224288099608827345377164375927559338153505991404973888594356664393487249819589915881178770048740
R.<x>=Zmod(y)[]
f=2019*x**2+2020*x**3+2021*x**4-num
f.roots()
#x=12131601165788024635030034921084070470053842112984866821070395281728468805072716002494427632757418621194662541766157553264889658892783635499016425528807741
注意这里的$ R.<x>=Zmod(y)[] $是在整数域上定义未知数$x$,并且方程必须化为$f(x)=0$的形式。可以参考SageMath常用函数。
求m
由于题目给了$dp$,容易想到可能是dp泄露,但是条件不够。正常的dp泄露攻击至少需要$dp$、$e$、$n$、$c$这四个参数,但是本题中没有给出$n$,但是经过一系列推导,我们仍然可以得出$c$、$dp$、$p$、$m$之间的关系,推导过程如下
由已知
$m^e \equiv c \mod n$ (1)
$dp \equiv d \mod (p-1)$ (2)
我们同时在(1)式两边平方dp,可得
$m^{(e*dp)} \equiv c^{dp} \mod n$
由于$n=p^4*q$,所以可得
$m^{(e*dp)} \equiv c^{dp} \mod p$
而
$e*dp=e*d \mod (p-1)$
$e*d \equiv 1 \mod (p-1)*(q-1)$
所以有
$e*dp \equiv e*d \mod (p-1)(q-1) \equiv e*d \mod (p-1) \equiv 1$
$k*(p-1)+1=e*dp$
带入上式
$c^{dp} \equiv m^{(k*(p-1)+1)} \mod p$
由费马小定理可知
$m^{(p-1)} \equiv 1 \mod p$
$m^{k*(p-1)} \equiv 1 \mod p$
最终可以得到
$c^{dp} \equiv m \mod p$
于是我们便得到了$c$、$dp$、$p$、$m$之间的关系,容易求出
from Crypto.Util.number import *
dp=379476973158146550831004952747643994439940435656483772269013081580532539640189020020958796514224150837680366977747272291881285391919167077726836326564473
c=57248258945927387673579467348106118747034381190703777861409527336272914559699490353325906672956273559867941402281438670652710909532261303394045079629146156340801932254839021574139943933451924062888426726353230757284582863993227592703323133265180414382062132580526658205716218046366247653881764658891315592607194355733209493239611216193118424602510964102026998674323685134796018596817393268106583737153516632969041693280725297929277751136040546830230533898514659714717213371619853137272515967067008805521051613107141555788516894223654851277785393355178114230929014037436770678131148140398384394716456450269539065009396311996040422853740049508500540281488171285233445744799680022307180452210793913614131646875949698079917313572873073033804639877699884489290120302696697425
p=12131601165788024635030034921084070470053842112984866821070395281728468805072716002494427632757418621194662541766157553264889658892783635499016425528807741
print(long_to_bytes(pow(c,dp,p)))Wilson
附件如下
from Crypto.Util.number import getPrime, bytes_to_long
from gmpy2 import next_prime
# length of flag is 37
p = getPrime(512)
q = next_prime(p)
f = open('flag.txt', 'rb')
flag = bytes_to_long(f.read())
f.close()
n = p * q
noise = 1
for i in range(1, p):
noise = (noise * i) % q
e = 65537
m = noise * flag % n
c = pow(m, e, n)
print(n)
print(c)
#n=100189599139045520692403514463438191919411159406336533264628466489136567106850053961211156503402646767637582308399326881242266939213884415929464845632614082572953261137505406070253764077806987137037034310296845793371123661392496824861923474884525612617707544570336505659782455487338427377348917874318463239257
#c=52162333124576686957153373769942403179822965367913494233622980146825418118797445630968150884296792193181121863149103395864786568453259110222784314675525339496760525297631678262500661476204948790654439464714409499209171376596016201182419029308570372822332848217278055720486674459768995713889509753949399299473题目考察的是威尔逊定理,常用于出现阶乘的情况下

注意到$p$、$q$十分接近,如果$p$、$q$相差过大或过小都容易被分解。可以选择在线网站或者yafu工具分解$n$。
此时根据noise的生成过程,我们可以求出noise的值,但是由于$p$的值过大,所需时间非常长。可以考虑使用Wilson定理,推导如下
要求$(p-1)! \mod q$,由于$p<q$,所以$(q-1)! \equiv (p-1)!*p*(p+1)*…*(q-1) \equiv -1 \mod q$。
由于$p$、$q$十分接近,所以我们容易求出$p*(p+1)*…*(q-1) \equiv x \mod q$。
此时我们有$(p-1)!*x \equiv -1 \mod q$,容易求出$(p-1)! \equiv noise \mod q$,求出noise后,便容易求出flag,脚本如下
from Crypto.Util.number import *
import gmpy2
p=10009475467727842964944136921466692066364373263024256649726700299397848867019210333658570624176497020220474895288449922932713775955785908704109113057682309
q=10009475467727842964944136921466692066364373263024256649726700299397848867019210333658570624176497020220474895288449922932713775955785908704109113057682373
n=100189599139045520692403514463438191919411159406336533264628466489136567106850053961211156503402646767637582308399326881242266939213884415929464845632614082572953261137505406070253764077806987137037034310296845793371123661392496824861923474884525612617707544570336505659782455487338427377348917874318463239257
c=52162333124576686957153373769942403179822965367913494233622980146825418118797445630968150884296792193181121863149103395864786568453259110222784314675525339496760525297631678262500661476204948790654439464714409499209171376596016201182419029308570372822332848217278055720486674459768995713889509753949399299473
phi=(p-1)*(q-1)
e = 65537
d=gmpy2.invert(e,phi)
noi=1
for i in range(p, q):
noi = (noi * i) % q
# print(noi)
noise=-1*gmpy2.invert(noi,q)%q
print(noise)
m=pow(c,d,n)
innoise=gmpy2.invert(noise,n)
print(innoise)
flag=long_to_bytes(pow(m*innoise,1,n))
print(flag)Fermat with Binomial
原题,附件如下 task.py
from Crypto.Util.number import *
f = open('flag.txt', 'rb')
m = bytes_to_long(f.read())
f.close()
e = 65537
p = getPrime(1024)
q = getPrime(1024)
n = p * q
c = pow(m, e, n)
hint1 = pow(2021 * p + q, 20212021, n)
hint2 = pow(1010 * p + 1011, q, n)
f = open('message.txt', 'w')
f.write(f'n={n}\n')
f.write(f'c={c}\n')
f.write(f'hint1={hint1}\n')
f.write(f'hint2={hint2}\n')
f.close()message.txt
n=16785815493192323072561202520621502124354484873141439416485516896177209180170954358917536655296832389378159385508553582292316986439935870611836481627326624997826278718936899131627405269577001541561786652522795230359038066756500166621870294967504124007392361309677236631475857268249665705586160191841238378747704555589725214417560311950480552359244858338836565084199965357719917862865124721829629583801017461751844801305560796234037169537157236798038347132037065583033136175781724971303334634074643113231202854595470566133689932557205673653855603056520355846208058018605770349841277407297822002222655287986001654291931
c=12824901853900928176431805967670922082099408423359348740734692908225214283313020989235896494342846615758839954388241321859784138067628962023114456647732896918446926075150525242914486413449921088854955092881525457824965211111708060188052025883249556408765110000416480911959539207515903372662706942051175602406993472605337450011214198253823995374918086046571064526610180657696977528863091044723572782646772325280660263920280922710139393502451340521170658459979145980603061780857907568888355186816350804498385690058379721372491179071169195852152316654113738209736216721551163445193680416946172818040555458013285013076026
hint1=9100042084582559120159031222877385918131627674965428834732092483610222485185500852690169889158524199071605287690845087305188994225784309780346317628828223709405785692567210943043233210503182916135218501703770962120690794212530724251491005258749274621926983941779357144111637154016600411666779133073494389367203037839113492716852468953430962340504727673205375932008380231967356987830939184941935559824751997435555229308732296050345353884892269792098915710385538823080718443304466681676033122340721360871484264707931485035700119764663528137240048303559376884120155943565064746404763004240115053288163324152157473617990
hint2=9715835317933770028352656960194612511232332508578016476234653979758738724483036248158492859699534774069055258691831221183554038938838861427968839315936796645021031146434403767322049813439272141318924746372792359202961866805563916806745433288822292142587118556212747743843666517677675229877703300490191424342819740469916571702460052662852376459432341889334300260369825585572770112675953798390556158097350576177067289449449873243010686716960572551733859485003137822891360533488207469003452641541262228655905655933669756058464699629520449342902123166997135656358968094821077563145658394017534114487847397469149938035501由hint1=pow(2021*p+q,20212021,n),$(2021*p+q)^{20212021} \equiv hint1 \mod n$
由二项式定理,中间项都出现$p*q$,能被$n$整除,原始转化为如下形式
$(2021*p)^{20212021}+q^{20212021} \equiv hint1 \mod n$
由hint2=pow(1010*p+1011,q,n),有$(1010*p+1011)^q \equiv hint2 \mod n$
有
$(1010*p+1011)^q \equiv hint2 \mod q $
由费马小定理$x^{p-1} \equiv 1 \mod p$,可得
$1010*p+1011 \equiv hint2 \mod q$
$k*q+ 1010*p+1011 =hint2$
$1010*p+k*q=hint2-1011 \mod n$
两边同时平方20212021
$(1010*p+k*q)^{20212021} \equiv (hint2-1011)^{20212021} \mod n$
$(1010*p)^{20212021}+(k*q)^{20212021} \equiv (hint2-1011)^{20212021} \mod n $
于是我们现在就有如下两式
$(2021*p)^{20212021}+q^{20212021} \equiv hint1 \mod n$
$(1010*p)^{20212021}+(k*q)^{20212021} \equiv (hint2-1011)^{20212021} \mod n $
现在我们来统一$p$的系数
$(2021*1010*p)^{20212021}+(1010*q)^{20212021} \equiv hint1*1010^{20212021} \mod n$
$(2021*1010*p)^{20212021}+(2021*k*q)^{20212021} \equiv (2021*(hint2-1011))^{20212021} \mod n $
两式相减消去$p$
$ ((2021*k-1010)*q)^{20212021} \equiv (2021*(hint2-1011))^{20212021}- hint1*1010^{20212021} \mod n $
$ ((2021*k-1010)*q)^{20212021} \equiv (2021*(hint2-1011))^{20212021}- hint1*1010^{20212021} \mod q $
上式显然为$q$的倍数,hint1和hint2已知,所以可以直接算出上式的值$x$,接着计算GCD(x,n)即为$p$的值。得出了$p$、$q$,易求flag,完整脚本如下
import gmpy2
from Crypto.Util.number import *
e=65537
n=16785815493192323072561202520621502124354484873141439416485516896177209180170954358917536655296832389378159385508553582292316986439935870611836481627326624997826278718936899131627405269577001541561786652522795230359038066756500166621870294967504124007392361309677236631475857268249665705586160191841238378747704555589725214417560311950480552359244858338836565084199965357719917862865124721829629583801017461751844801305560796234037169537157236798038347132037065583033136175781724971303334634074643113231202854595470566133689932557205673653855603056520355846208058018605770349841277407297822002222655287986001654291931
c=12824901853900928176431805967670922082099408423359348740734692908225214283313020989235896494342846615758839954388241321859784138067628962023114456647732896918446926075150525242914486413449921088854955092881525457824965211111708060188052025883249556408765110000416480911959539207515903372662706942051175602406993472605337450011214198253823995374918086046571064526610180657696977528863091044723572782646772325280660263920280922710139393502451340521170658459979145980603061780857907568888355186816350804498385690058379721372491179071169195852152316654113738209736216721551163445193680416946172818040555458013285013076026
hint1=9100042084582559120159031222877385918131627674965428834732092483610222485185500852690169889158524199071605287690845087305188994225784309780346317628828223709405785692567210943043233210503182916135218501703770962120690794212530724251491005258749274621926983941779357144111637154016600411666779133073494389367203037839113492716852468953430962340504727673205375932008380231967356987830939184941935559824751997435555229308732296050345353884892269792098915710385538823080718443304466681676033122340721360871484264707931485035700119764663528137240048303559376884120155943565064746404763004240115053288163324152157473617990
hint2=9715835317933770028352656960194612511232332508578016476234653979758738724483036248158492859699534774069055258691831221183554038938838861427968839315936796645021031146434403767322049813439272141318924746372792359202961866805563916806745433288822292142587118556212747743843666517677675229877703300490191424342819740469916571702460052662852376459432341889334300260369825585572770112675953798390556158097350576177067289449449873243010686716960572551733859485003137822891360533488207469003452641541262228655905655933669756058464699629520449342902123166997135656358968094821077563145658394017534114487847397469149938035501
qn=gmpy2.powmod(1010,20212021,n)*hint1-gmpy2.powmod((2021*(hint2-1011)),20212021,n)
p=gmpy2.gcd(qn,n)
print(p)
q=n//p
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
print(long_to_bytes(gmpy2.powmod(c,d,n)))silent_peeper
附件如下
from Crypto.Util.number import *
from Crypto.Cipher import AES
import binascii
flag = "flag{XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX}"
bs = AES.block_size
pad = lambda s: s + (bs - len(s) % bs) * chr(bs - len(s) % bs)
p = 174807157365465092731323561678522236549173502913317875393564963123330281052524687450754910240009920154525635325209526987433833785499384204819179549544106498491589834195860008906875039418684191252537604123129659746721614402346449135195832955793815709136053198207712511838753919608894095907732099313139446299843
g = 41899070570517490692126143234857256603477072005476801644745865627893958675820606802876173648371028044404957307185876963051595214534530501331532626624926034521316281025445575243636197258111995884364277423716373007329751928366973332463469104730271236078593527144954324116802080620822212777139186990364810367977
a = getRandomNBitInteger(40)
b = getRandomNBitInteger(40)
A = pow(g, a, p)
B = pow(g, b, p)
assert pow(A, b, p) == pow(B, a, p)
key = pow(A, b ,p)
key = long_to_bytes(key)[:16]
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = cipher.encrypt(pad(flag))
with open('cipher', 'w') as f:
f.write("A, B = {}\n".format(str((A, B))))
f.write("ciphertext = {}\n".format(binascii.hexlify(ciphertext)))
f.close()使用AES加密flag,但是加密的key也被加密,易知key=pow(g,ab,p)。但是$a$、$b$为随机数,并且求$a$、$b$为离散对数难题。但注意到$a$、$b$的长度为40位,缩小了求解范围,可以使用sage的discrete_log_lambda()函数进行求解,脚本如下
sage
G=GF(17480715736546509273132356167852223654917350291331787539356496312333028105252468745075491
....: 0240009920154525635325209526987433833785499384204819179549544106498491589834195860008906875039
....: 4186841912525376041231296597467216144023464491351958329557938157091360531982077125118387539196
....: 08894095907732099313139446299843)
sage: g=G(418990705705174906921261432348572566034770720054768016447458656278939586758206068028761736
....: 4837102804440495730718587696305159521453453050133153262662492603452131628102544557524363619725
....: 8111995884364277423716373007329751928366973332463469104730271236078593527144954324116802080620
....: 822212777139186990364810367977)
sage: A=G(142989488568573584455487421652639325256968267580899511353325709765313839485530879575182195
....: 3918471066110589866467587395058203504168107542595229494024284854564318842231616901323856050387
....: 6758243107087513867861243598342550027303880758206976345599448636599336649947841278322005275359
....: 7397455113133312907456163112016)
sage: B=G(166317004001833296087921124420385439115638296991950248194084106124906713557397285109441678
....: 5217085345783011123322425762267729634575751669180241126492894380962255672331531058187144732513
....: 9349242754287009766402650270061476954875266747743058962546605854650101122523183742112737784691
....: 464177427011570888040416109544L)
sage: discrete_log_lambda(A,g,(2^39,2^41))
822690494337
sage: discrete_log_lambda(B,g,(2^39,2^41))
621209248538求出$a$、$b$后,易求flag
from Crypto.Util.number import *
from Crypto.Cipher import AES
import binascii
import sympy
A,B=142989488568573584455487421652639325256968267580899511353325709765313839485530879575182195391847106611058986646758739505820350416810754259522949402428485456431884223161690132385605038767582431070875138678612435983425500273038807582069763455994486365993366499478412783220052753597397455113133312907456163112016,16631700400183329608792112442038543911563829699195024819408410612490671355739728510944167852170853457830111233224257622677296345757516691802411264928943809622556723315310581871447325139349242754287009766402650270061476954875266747743058962546605854650101122523183742112737784691464177427011570888040416109544
ciphertext=0xed5c68ebb65aa3a13afb259cf3984ce60bdc54b7ef918b850745df850cf4c450b02216c0c6e67ed501a17e516496cd6c
p=174807157365465092731323561678522236549173502913317875393564963123330281052524687450754910240009920154525635325209526987433833785499384204819179549544106498491589834195860008906875039418684191252537604123129659746721614402346449135195832955793815709136053198207712511838753919608894095907732099313139446299843
g=41899070570517490692126143234857256603477072005476801644745865627893958675820606802876173648371028044404957307185876963051595214534530501331532626624926034521316281025445575243636197258111995884364277423716373007329751928366973332463469104730271236078593527144954324116802080620822212777139186990364810367977
a=822690494337
b=621209248538
key = pow(A, b ,p)
key=long_to_bytes(key)[:16]
aes=AES.new(key,AES.MODE_ECB)
flagpad=aes.decrypt(long_to_bytes(int(ciphertext)))
print(flagpad)关于sage中求解离散对数,可以参考Sage离散对数求解。
Misc
squid_game
查看下载的文件,为JSFuck加密,网站在线解密即可。或者直接F12在浏览器控制台运行。

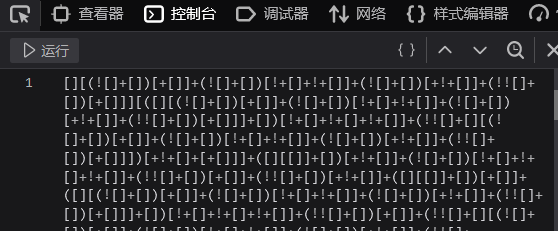
Hamburger Souls
使用010editor查看文件,发现jpg文件头FF D8,将文件后缀改为.jpg。010中搜索文本CTF即可
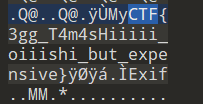
xorQR_CODE
标题上有xor,实际上和xor没有关系。打开.txt文件,由-和,组成,可分别将其当作二进制数据01。
使用Python查看其长度为67600,开方恰好为260*260。编写脚本绘图
from PIL import Image
serc=[]
with open("secret.txt",'r') as f:
serc=f.readlines()
# print(len(serc[0]))
image=Image.new('L',(260,260),255)
for a in range(260):
for b in range(260):
if serc[0][a*260+b]==',':
image.putpixel((a,b),0)
image.show()结果如下

EasyPcap
A network diagnose operation was conducted and this act was captured. Find the IP operated and the command. Flag is expected to be 3DES encrypt hex result(text is IP,key is command). Use MyCTF{} to warp your flag.
寻找出数据流中用于网络诊断的命令,并以IP地址作为明文,命令作为密钥进行3DES加密。Flag为加密结果的十六进制。
仔细分析可以发现数据包中包含ICMP协议,它用于在IP主机、路由器之间传递控制消息。最常见的命令就是ping命令,常用于检测主机之间的连通性。

ping命令常使用ICMP协议向目标主机发送Echo request报文,目标主机在收到Echo报文后会返回一个Echo reply包作为响应。ping命令常用的格式为ping ip [-n 包大小] [-l 包长度] [-t (无限发包)]。
很明显,这里使用的网络诊断命令为ping,源地址为192.168.0.106,目标地址为185.199.108.153。
于是我们使用185.199.108.153作为明文,ping作为密文进行3DES加密,输出为十六进制。

Strobe Memory
my pwd,and message(RC4 encrypted) in memory
内存取证题目,可以使用volatility工具进行内存分析。
首先判断镜像文件需要的profile,volatility -f memdump.mem imageinfo
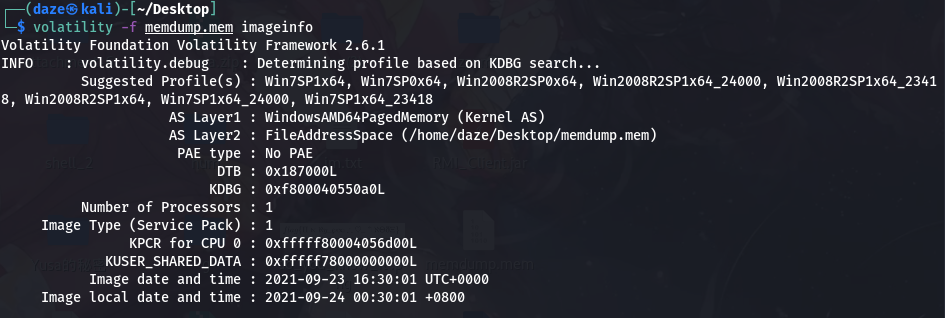
接着查看内存镜像中的进程,volatility -f memdump.mem --profile=Win7SP1x64 pslist
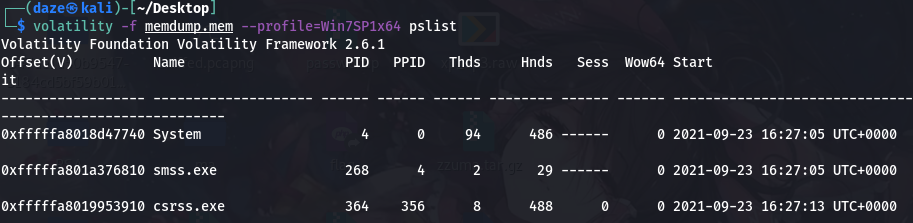
发现cmd.exe

查看历史cmd命令,volatility -f memdump.mem --profile=Win7SP1x64 cmdscan
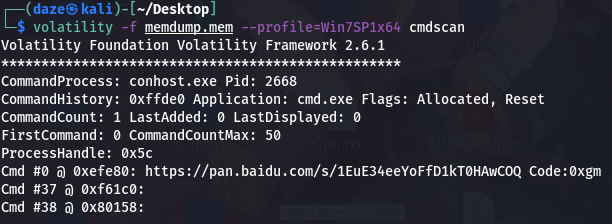
发现网盘链接,这应该就是message了,复制下来
U2FsdGVkX19zSBh5Q4NEBQ3Y/IE3kqcTeB38/QUfJPjz3MYZo8//WjjcQafUU00Q
gHsaQRRvQnwdai4mXf0IZDUBciEAMT1wrhRi1nVamcKU6X6Os4XlKYFu2R9UkS/A
eBJssMKWwZS7+SMwJA+4eH3Sqxr6OHKAUm3u4qj76x2Cmpo7TgBTQ1TzQtvbR6VY
qcxV9qPIR+8QZ/TeDZIscZPxpwg+urOCL97OOFMxt79Cby5z2fP0XzCxUWnVmO3v
oCvJVJ2bYoYqpTqOo6xzH47zYQA2kSjuSxP6x33SheV3IDPpmdeSWPssARLNd971
cCJbHBs1Wlhh7SzC7hKYxLO1/AGIDkVKFCO3M92/BQ+71tQNSQ7GQwqWhtOmxOqk
H3vzxFewwbrrhVKdq8decfV0VKcHTwjOa9sr/VY5hCzUoxPyerHvspvQ0nJlTL+Q
3RDUp8cZwb+GYgYEs8zl9CpBRqXynDjVgRt6L4bJKSaaeidyCwAILAvGUtrnliP1
1hvMEoUL1BoRPZapa4/XZfeowmJYBxCdNbtYQvJTmFxD1JUZQDgu+ARslPHnsrrl
HMHqSpWlHu0AYNEu990IESIjsMTkUuBXd9CuHIDsbVGdiWsAorf78osvoIB+oaUJ
8B8Vg03Bty8RRW4qCD9OSF1PiP4p6SDVt+AJWYwV3bTBA26+zbr3fZBwX9fcQhX5
kwXxc88wj9wKX1DTEfjD4/On现在我们需要寻找密码,考虑可能是Windows用户密码,使用passware kit forensic工具进行破解
选择Memory Analysis-Windows User,破解结果如下,密码为ffxiv
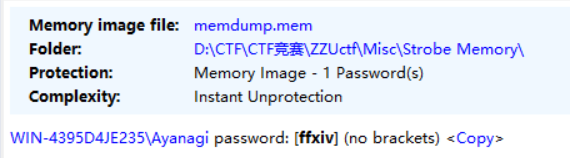
提示为RC4加密,使用ffxiv作为密钥,解密结果如下
tupper
127599739933967093131152452092967203715004268819324601877203708695092905539879766254380351824119433309450605219662669705322879039288406079685894700876853939343546466674167675843632299107885531659513226127945849860968719044332851963670087790025283685279148683566101822541616548816014089018681570665376678752577639305155890047680270412789170315331023708437508890804843297418167809379868869838323658337305551758361448088050669051796954650620349250879619020031969406174600372916970856329970323239288072622245492457530770587648提示tupper,经搜索之后是Tupper自我指涉公式造图,寻找一个脚本解密即可,将参数$k$替换成以上大数即可,解密结果如下
翻转之后可得Flag。
只是个PNG,别想太多了.png
使用binwalk查看文件,发现有隐藏文件,使用binwalk -e PNG.png进行分离
查看分离文件得到flag