AES

概述

AES（Advanced Encryption Standard），在密码学中又称Rijndael加密法，是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES，已经被多方分析且广为全世界所使用。经过五年的甄选流程，高级加密标准由美国国家标准与技术研究院（NIST）于2001年11月26日发布于FIPS PUB 197，并在2002年5月26日成为有效的标准。2006年，高级加密标准已然成为对称密钥加密中最流行的算法之一

高级加密标准(AES,Advanced Encryption Standard)是密码学中的高级加密标准，AES为分组加密法，把明文分成一组一组的，每组长度相等，每次加密一组数据，直到加密完整个明文，在AES标准规范中，分组长度只能是128位，AES是按照字节进行加密的，也就是说每个分组为16个字节（每个字节8位）。密钥的长度可以使用128位、192位或256位。这导致密钥长度不同，推荐加密的轮数也不同。

加解密流程

算法各部分的作用与意义

• 明文P

没有经过加密的数据

• 密钥K

用来加密明文的密码，在对称加密算法中，加密与解密的密钥是相同的。密钥为接收方与发送方协商产生，但不可以直接在网络上传输，否则会导致密钥泄漏，通常是通过非对称加密算法加密密钥，然后再通过网络传输给对方，或者直接面对面商量密钥。密钥是绝对不可以泄漏的，否则会被攻击者还原密文，窃取机密数据

• AES加密函数

设AES加密函数为E，则 C = E(K, P),其中P为明文，K为密钥，C为密文。也就是说，把明文P和密钥K作为加密函数的参数输入，则加密函数E会输出密文C

• 密文C

经加密函数处理后的数据

• AES解密函数

设AES解密函数为D，则 P = D(K, C),其中C为密文，K为密钥，P为明文。也就是说，把密文C和密钥K作为解密函数的参数输入，则解密函数会输出明文P

实际中，一般是通过RSA加密AES的密钥，传输到接收方，接收方解密得到AES密钥，然后发送方和接收方用AES密钥来通信。

工作模式

• 电码本模式（Electronic Codebook Book (ECB)）
• 密码分组链接模式（Cipher Block Chaining (CBC)）
• 计算器模式（Counter (CTR)）
• 密码反馈模式（Cipher FeedBack (CFB)）
• 输出反馈模式（Output FeedBack (OFB)）

AES的加密标准

在AES标准规范中，分组长度只能是128位，也就是说，每个分组为16个字节（每个字节8位）。密钥的长度可以使用128位、192位或256位，如果数据块及密钥长度不足时会补齐。密钥的长度不同，推荐加密轮数也不同，如下表所示

AES	密钥长度（32位比特字）	分组长度(32位比特字)	加密轮数
AES-128	4	4	10
AES-192	6	4	12
AES-256	8	4	14

AES算法流程分析

这里介绍的是AES-128，也就是密钥的长度为128位，加密轮数为10轮。

AES的加密公式为C = E(K,P)，在加密函数E中，会执行一个轮函数，并且执行10次这个轮函数，这个轮函数的前9次执行的操作是一样的，只有第10次有所不同。也就是说，一个明文分组会被加密10轮。AES的核心就是实现一轮中的所有操作。

明文矩阵填充

AES的处理单位是字节，128位的输入明文分组P和输入密钥K都被分成16个字节，分别记为P = P0 P1 … P15 和 K = K0 K1 … K15。如，明文分组为P = abcdefghijklmnop,其中的字符a对应P0，p对应P15。一般地，明文分组用字节为单位的正方形矩阵描述，称为状态矩阵。在算法的每一轮中，状态矩阵的内容不断发生变化，最后的结果作为密文输出。该矩阵中字节的排列顺序为从上到下、从左至右依次排列。

密钥矩阵填充

类似地，128位密钥也是用字节为单位的矩阵表示，矩阵的每一列被称为1个32位比特字。通过密钥编排函数该密钥矩阵被扩展成一个44个字组成的序列W[0],W[1], … ,W[43],该序列的前4个元素W[0],W[1],W[2],W[3]是原始密钥，用于加密运算中的初始密钥加（下面介绍）;后面40个字分为10组，每组4个字（128比特）分别用于10轮加密运算中的轮密钥加。后面10组密钥通过初始密钥进行密钥扩展得到。

加解密流程

AES加解密主要有以下几步操作，完整的加解密流程是通过循环以下步骤来完成的，具体如下图表示

• 轮密钥加
• 字节代换
• 行位移
• 列混合

加解密步骤分析

字节代换

AES的字节代换其实就是通过一个简单的查表操作来进行非线性运算。AES定义了一个S盒和一个逆S盒。分别用来加解密操作。

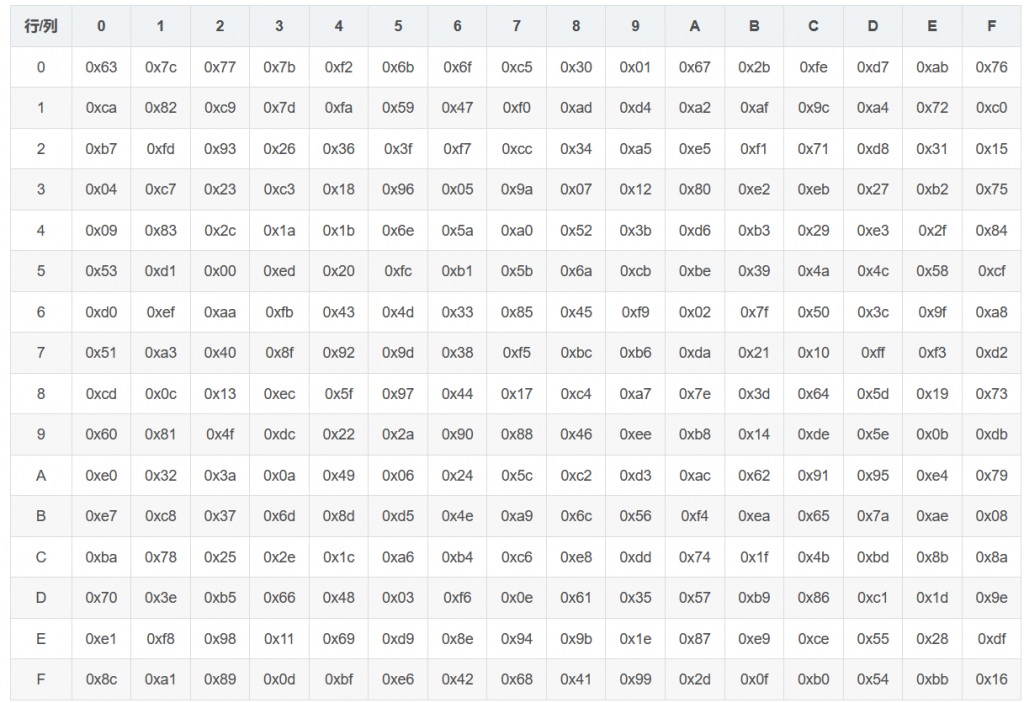
状态矩阵中的元素按照下面的方式映射为一个新的字节：把该字节的高4位作为行值，低4位作为列值，取出S盒或者逆S盒中对应的行的元素作为输出。例如，加密时，输出的字节S1为0x12,则查S盒的第0x01行和0x02列，得到值0xc9,然后替换S1原有的0x12为0xc9。状态矩阵经字节代换后的图如下

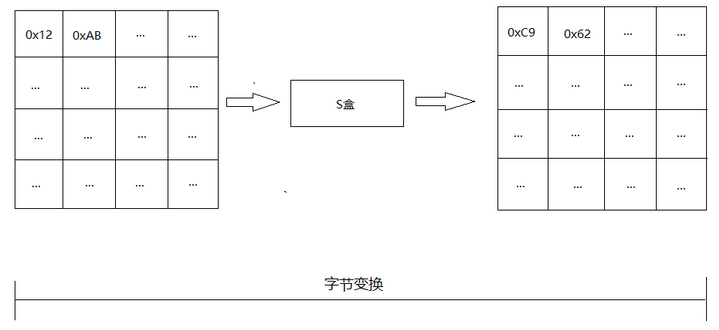
逆字节代换也就是查逆S盒来变换，逆S盒如下

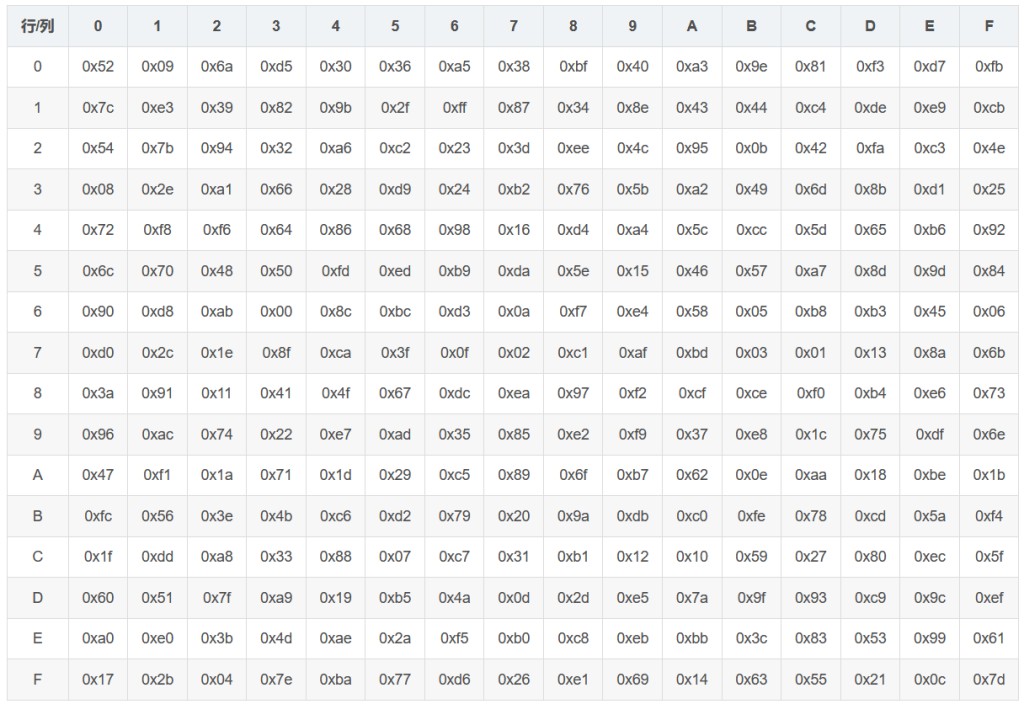
行位移

行移位是一个简单的左循环移位操作。当密钥长度为128比特时，状态矩阵的第0行左移0字节，第1行左移1字节，第2行左移2字节，第3行左移3字节，如下图所示

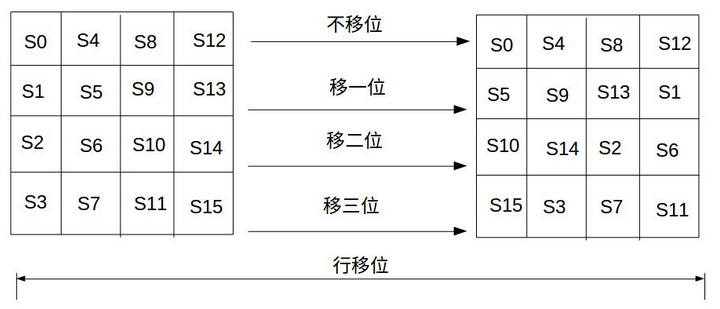
行位移的逆变换是将状态矩阵中的每一行执行相反的移位操作，例如AES-128中，状态矩阵的第0行右移0字节，第1行右移1字节，第2行右移2字节，第3行右移3字节。

列混合

列混合变换是通过矩阵相乘来实现的，经行移位后的状态矩阵与固定的矩阵相乘，得到混淆后的状态矩阵，如下图的公式所示

状态矩阵中的第j列(0 ≤j≤3)的列混合可以表示为下图所示

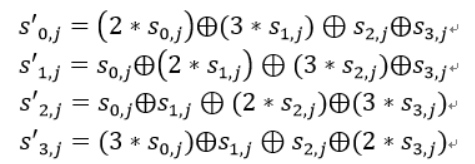
其中，矩阵元素的乘法和加法都是定义在基于GF(2^8)上的二元运算,并不是通常意义上的乘法和加法。

逆向列混合变换同样可由下图的矩阵乘法定义

轮密钥加

轮密钥加是将128位轮密钥Ki同状态矩阵中的数据进行逐位异或操作，如下图所示。其中，密钥Ki中每个字W[4i],W[4i+1],W[4i+2],W[4i+3]为32位比特字，包含4个字节，他们的生成算法下面在下面介绍。轮密钥加过程可以看成是字逐位异或的结果，也可以看成字节级别或者位级别的操作。也就是说，可以看成S0 S1 S2 S3 组成的32位字与W[4i]的异或运算。

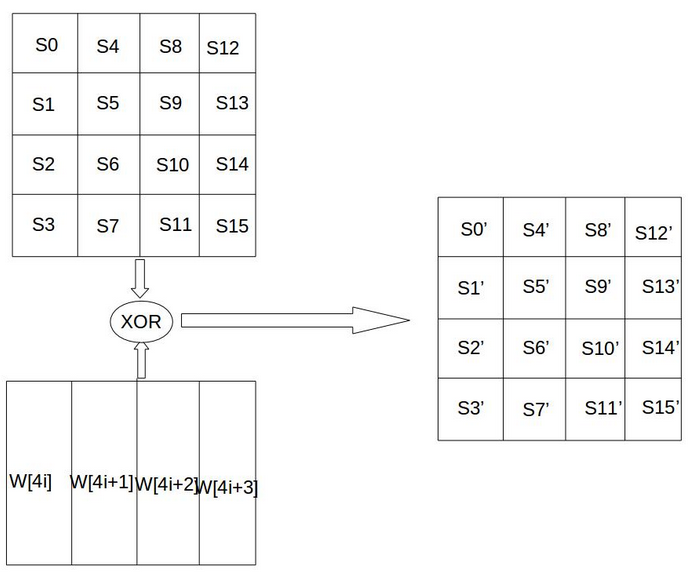
密钥扩展

AES首先将初始密钥输入到一个4×4的状态矩阵中，如下图所示

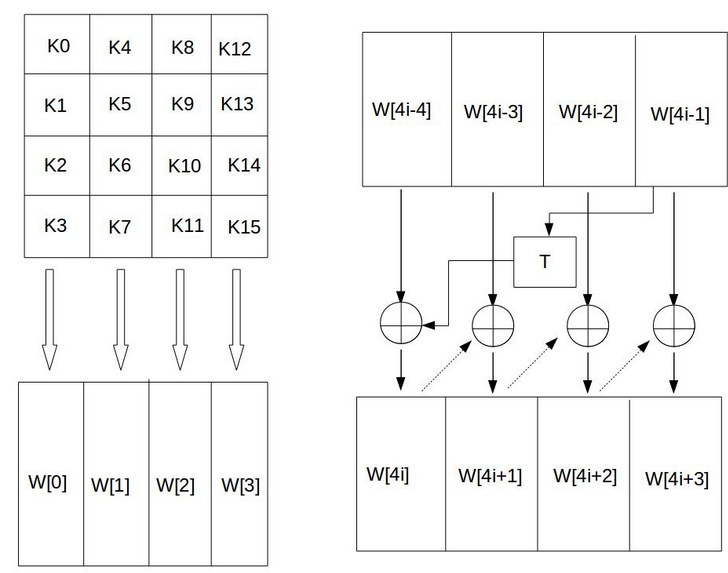
4×4矩阵的每一列的4个字节组成一个字，矩阵4列的4个字一次命名为W[0]、W[1]、W[2]和W[3]，它们构成一个以字为单位的数组W。

接着，对W数组扩充40个新列，构成总共44列的扩展密钥数组。新列以如下的递归方式产生

1. 如果i不是4的倍数，那么第i列由如下等式确定：
   $W[i]=W[i-4]⨁W[i-1]$
2. 如果i是4的倍数，那么第i列由如下等式确定：
   $W[i]=W[i-4]⨁T(W[i-1])$

T是一个有点复杂的函数，由3部分组成：字循环、字节代换和轮常量异或，这3部分的作用分别如下

1. 字循环：将1个字中的4个字节循环左移1个字节。即将输入字[b0, b1, b2, b3]变换成[b1,b2,b3,b0]
2. 字节代换：对字循环的结果使用S盒进行字节代换
3. 轮常量异或：将前两步的结果同轮常量Rcon[j]进行异或，其中j表示轮数

轮常量Rcon[j]是一个字，其值见下表

j	1	2	3	4	5
Rcon[j]	01 00 00 00	02 00 00 00	04 00 00 00	08 00 00 00	10 00 00 00
j	6	7	8	9	10
Rcon[j]	20 00 00 00	40 00 00 00	80 00 00 00	1B 00 00 00	36 00 00 00

DES

概述

DES数据加密标准（Data Encryption Standard）是发明最早的最广泛使用的分组对称加密算法。DES 加密算法中，明文和密文为 64bit分组，也就是8字节。密钥的长度为 64 位，但是密钥的每个第八位设置为奇偶校验位，因此密钥的实际长度为56位。

DES的结构

DES的基本结构是由Horst Feistel设计的，因此也叫Feistel网络、Feistel 结构 或者Feistel密码。很多密码算法中都用到这种结构。

加密流程

DES 加密算法大致分为 3 个步骤

1. 初始置换IP，用于重排明文分组的64比特数据
2. 迭代，16轮相同的变换，每轮中都有置换和代换运算
3. 逆初始置换IP^-1

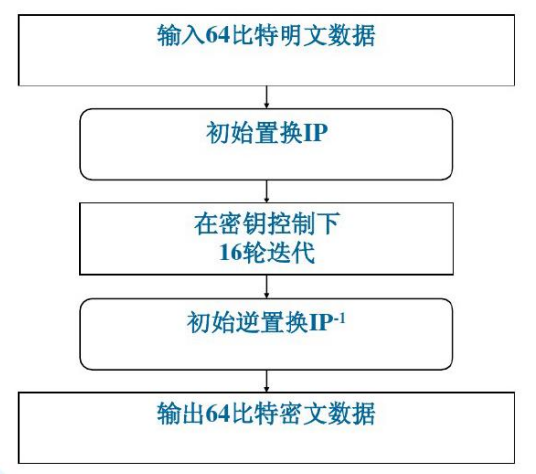
DES加密步骤分析

初始置换

初始置换是将原始明文M通过一张IP置换表进行处理得到置换明文M’。这里的置换只是将数据的位置进行变化，得到一个新的数据。IP 和IP^-1在密码意义上作用不大，它们的作用在于打乱原来输入明文x的ASCII码字划分的关系。

初始逆置换表和初始置换表是相互可逆的，就是将原来的数据的位置进行还原。置换过程如图

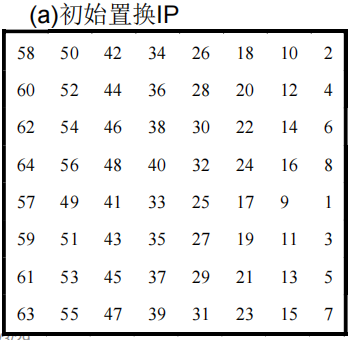
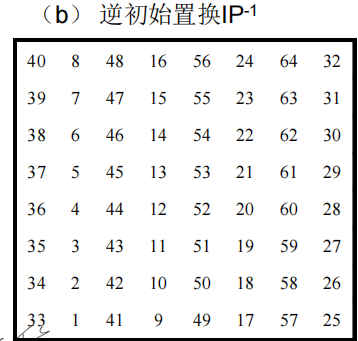
迭代

在Feistel网络中，加密的各个步骤称之为轮，整个加密过程就是进行若干次轮的循环。DES 是一种16轮迭代循环的Feistel网络，每轮变换可由以下公式表示：

$L_i=R_{i-1}$

$R_i=L_{i-1} \bigoplus F(R_{i-1},K_i)$

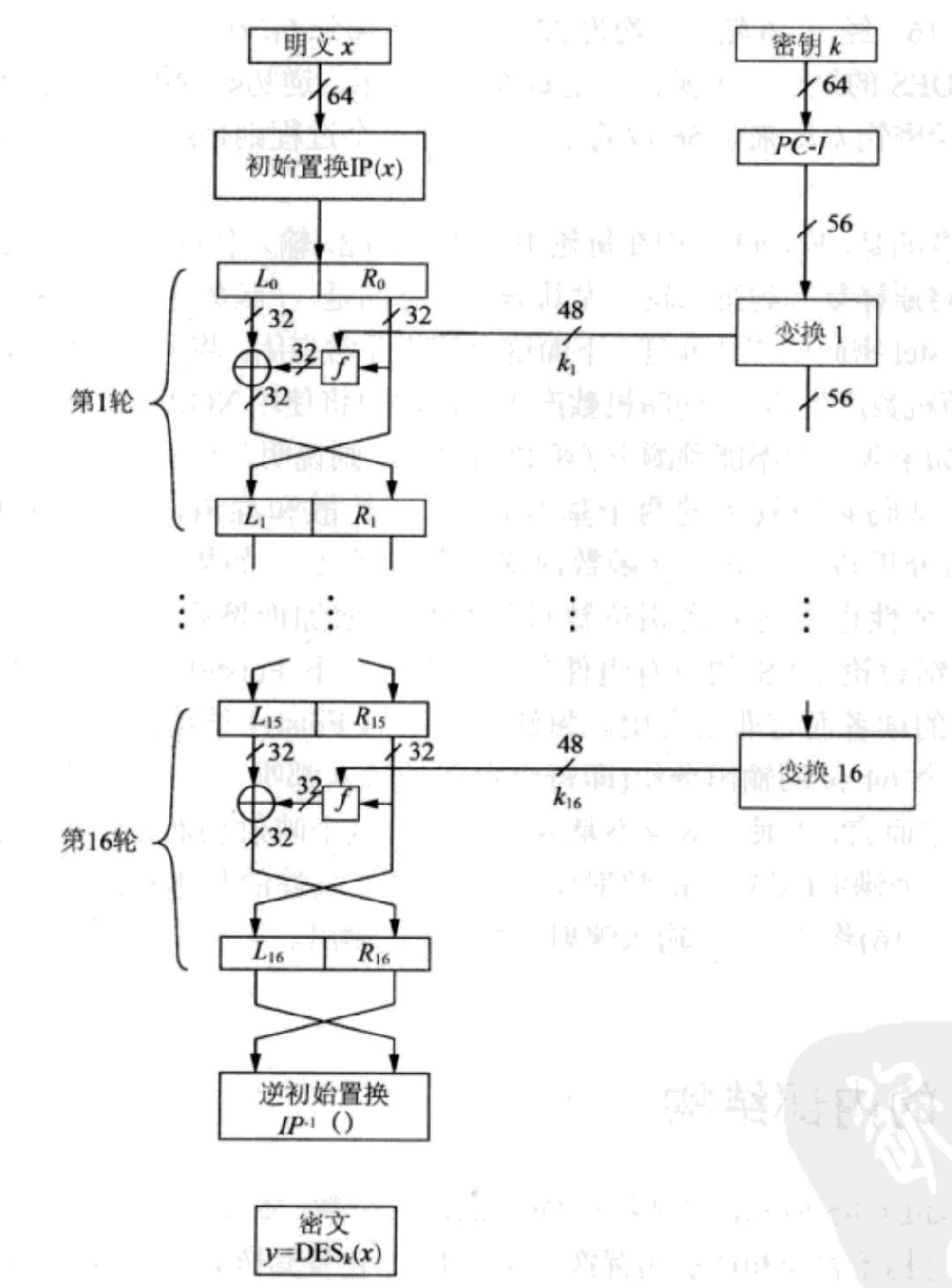
子密钥生成

其中每轮的48bit子密钥也叫轮密钥，DES 加密共执行16次迭代，每次迭代过程的数据长度为48位，因此需要16个48位的子密钥来进行加密，生成子密钥K_i的过程如下

K为长度64bit的串，其中56位是密钥，8位是奇偶校验位，在密钥的计算中，这些校验位可以略去。

子密钥产生过程如下

1. 算法输入56bit密钥
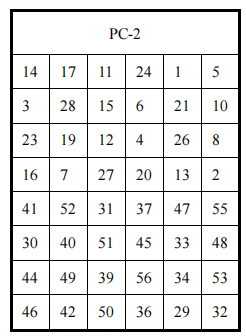
2. 首先经过一个置换运算，由表(a)PC-1给出
3. 然后将置换后的56bit分为各为28bit的左右两半，分别记为C₀和D₀
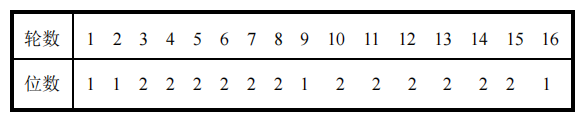
4. 在第i轮分别对C_i-1和D_i-1进行左循环位移，所位移数由表(c)给出。使用这种编排，子密钥寄存器的内容经16次迭代之后又回到原来的位置
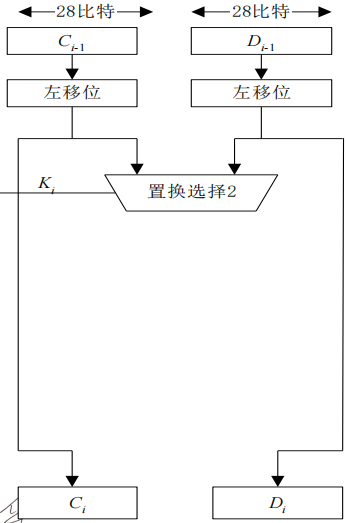
5. 移位后的结果做为求下一轮子密钥的输入，同时也作为置换选择2的输入
6. 通过表(b)PC-2的置换选择2产生的48bit的Ki，即为本轮的子密钥，作为函数$F(R_{i-1},K_i)$的输入

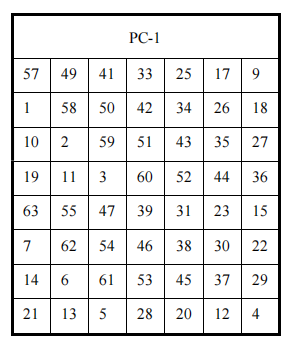
轮函数F

轮函数由四个处理过程组成

1. E扩展置换
2. 异或运算
3. S替代
4. P置换

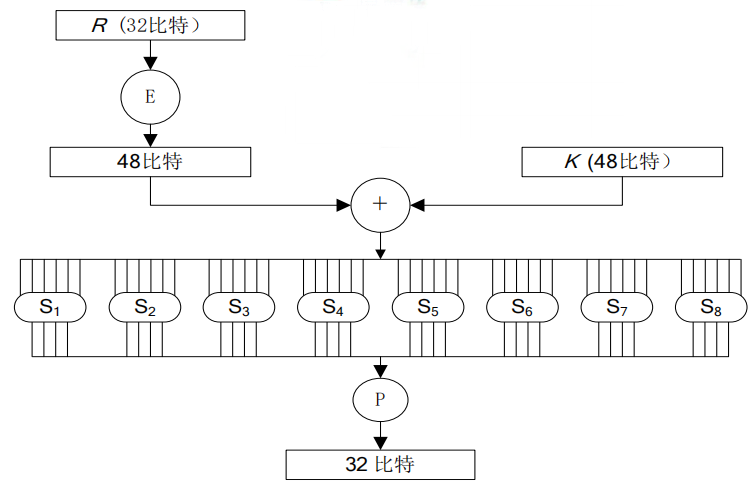
轮函数处理过程

1. 轮输入R为32bit
2. R首先被扩展成48比特，扩展过程由表（a）选择扩展运算E 定义，其中将R的16个比特各重复一次
3. 扩展后的48比特再与子密钥K_i异或
4. 然后再通过一个S盒，产生32比特的输出
5. 该输出再经过一个由表（b）置换运算P定义的置换， 产生的结果即为函数$F(R,K)$

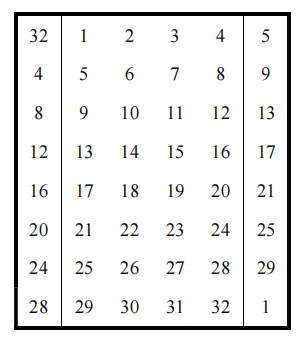
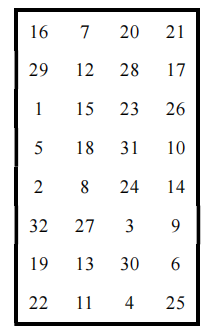
扩展方式：

1. 将输入的32bit每4bit为一组分为8块
2. 分别将第m-1块的最右bit和第m+1块的最左bit添加到第m块的左边和右边，形成输出的第m各6bit块

通过这种方式扩展，硬件实现较为简单

DES轮函数——S盒

轮函数中的代换由8个S盒组成。轮函数通过S盒将48比特压缩到32比特，每个S盒的输入长为6比特、输出长为4比特。每个S盒给出了4个代换（由一个表的4行给 出） ，行为2比特、列为4比特（共6比特）。

S盒作为该密码体制的唯一非线性组件对安全性至关重要。提供了密码算法所必须的混乱作用。并且S盒要求非线性度、差分均匀性、严格雪崩准则、 可逆性、没有陷门等。

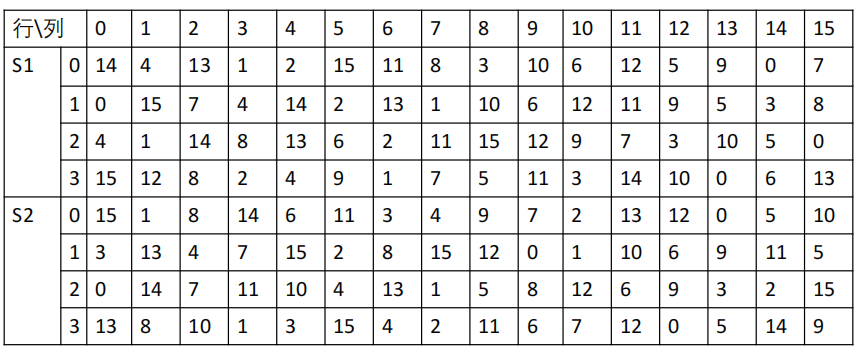
DES轮函数——P盒

将S盒变换后的32bit数据再进行P盒置换，置换后得到的32bit即为f函数的输出。

P盒特点

• P盒的各输出块的4各比特都来自不同的输入块
• P盒的各输入块的4个比特都分配到不同的输出块中
• P盒的第t输出块的4个比特都不来自第t输入块

使用方法

• 对每个盒Si，其6比特输入中，第1个和第6个比 特形成一个2位二进制数，用来选择Si的四个代 换中的一个
• 6比特输入中，中间4位用来选择列
• 行和列选定后，得到其交叉位置的十进制数， 表示为4位二进制数即得这一S盒的输出

初始逆置换IP^-1

经过16轮迭代之后，将两边的32bit密文合并成64bit置换输入，然后使用初始逆置换表进行逆置换得到64bit密文。

DES解密

和Feistel密码一样，DES的解密和加密使用同一算法， 但子密钥使用的顺序相反。

DES的解密过程可以描述为

$R_{i-1}=L_i$

$L_{i-1}=R_i \bigoplus f(L_i,K_i) i=16,15,…,1$

解密结构与加密结构完全相同，只不过是所使用的子密钥的顺序正好相反！

加密子密钥：$k_1,k_2,…,k_{15},k_{16}$

解密子密钥：$k_{16},k_{15},…,k_2,k_1$

分组加密中的工作模式

分组加密算法是按分组大小来进行加解密操作的，如DES算法的分组是64位，而AES是128位，但实际明文的长度一般要远大于分组大小，这样的情况如何处理呢？这正是”mode of operation”即工作模式要解决的问题：明文数据流怎样按分组大小切分，数据不对齐的情况怎么处理等等。早在1981年，DES算法公布之后，NIST在标准文献FIPS 81中公布了4种工作模式

• 电子密码本：Electronic Code Book Mode (ECB)
• 密码分组链接：Cipher Block Chaining Mode (CBC)
• 密文反馈：Cipher Feedback Mode (CFB)
• 输出反馈：Output Feedback Mode (OFB)

2001年又针对AES加入了新的工作模式

• 计数器模式：Counter Mode (CTR)

后来又陆续引入其它新的工作模式。在此仅介绍几种常用的

ECB：电子密码本模式（electronic codebook mode）

ECB模式只是将明文按分组大小切分，然后用同样的密钥正常加密切分好的明文分组。像一个密码本一样，明文和密文是一一对应的。

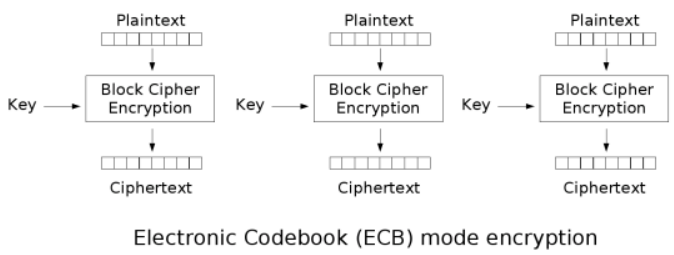
ECB的理想应用场景是短数据（如加密密钥）的加密。此模式的问题是无法隐藏原明文数据的模式，因为同样的明文分组加密得到的密文也是一样的。

从ECB的工作原理可以看出，如果明文数据在等分后，两块数据相同则会产生相同的加密数据块，这会辅助攻击者快速判断加密算法的工作模式，而将攻击资源聚集在破解某一块数据即可，一旦成功则意味着全文破解，大大提升了攻击效率。为了解决这一缺陷，设计者提出了更多的分组密码工作模式，这些模式下各组数据的加密过程彼此产生关联，尽最大可能混淆数据。

CBC：密码分组链接模式（cipher block chaining Triple）

此模式是1976年由IBM所发明，引入了IV初始向量（初始向量：Initialization Vector）的概念。IV是长度为分组大小的一组随机，通常情况下不用保密，不过在大多数情况下，针对同一密钥不应多次使用同一组IV。 CBC要求第一个分组的明文在加密运算前先与IV进行异或；从第二组开始，所有的明文先与前一分组加密后的密文进行异或。

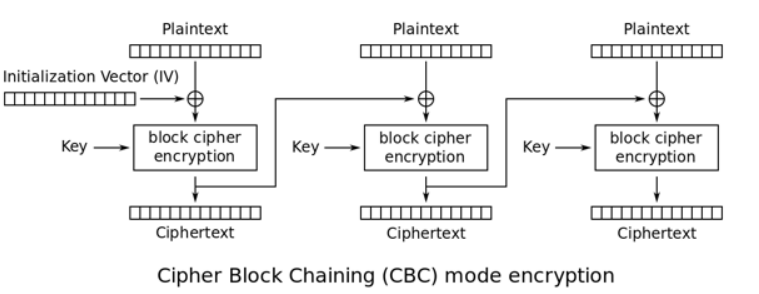
解密过程刚好相反，第一组密文在解密之后与初始向量IV异或得到第一组明文。第二组密文解密之后和第一组密文异或得到第二组明文。也就是说，解密一组明文需要本组和前一组的密文。

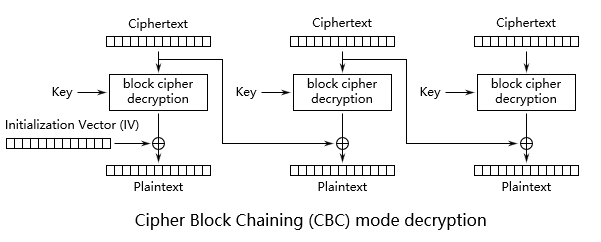
CBC模式相比ECB实现了更好的模式隐藏，但因为其将密文引入运算，加解密操作无法并行操作。同时引入的IV向量，并且还需要加、解密双方共同知晓方可。

CFB：密文反馈模式（Cipher FeedBack）

与CBC模式类似，但不同的地方在于，CFB模式先生成密码流字典，然后用密码字典与明文进行异或操作并最终生成密文。后一分组的密码字典的生成需要前一分组的密文参与运算。

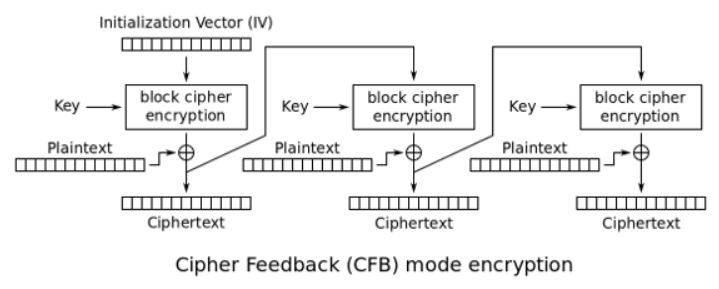
CFB模式是用分组算法实现流算法，明文数据不需要按分组大小对齐。

OFB：输出反馈模式（Output Feedbaek）

OFB模式与CFB模式不同的地方是：生成字典的时候会采用明文参与运算，CFB采用的是密文。

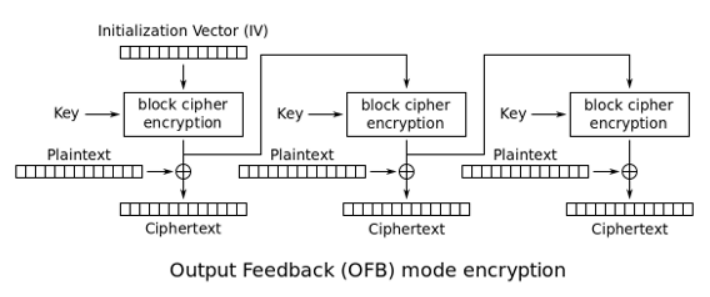
CTR：计数器模式（counter mode）

上面的几种工作模式都存在一个共性：数据块彼此之间关联，当前块的解密依赖前面的密文块，因此不能随机访问任意加密块。这样会使得用户为了获取其中一点数据而不得不解密所有数据，当数据量大时效率较低。

CTR模式同样会产生流密码字典，但同是会引入一个计数器，以保证任意长时间均不会产生重复输出。

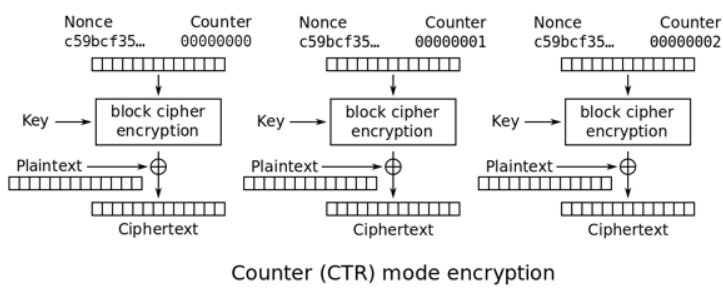
CTR模式只需要实现加密算法以生成字典，明文数据与之异或后得到密文，反之便是解密过程。CTR模式可以采用并行算法处理以提升吞量，另外加密数据块的访问可以是随机的，与前后上下文无关。

CCM：Counter with CBC-MAC

CCM模式，全称是Counter with Cipher Block Chaining-Message Authentication Code，是CTR工作模式和CMAC认证算法的组合体，可以同时数据加密和鉴别服务。

明文数据通过CTR模式加密成密文，然后在密文后面再附加上认证数据，所以最终的密文会比明文要长。具体的加密流程如下描述：先对明文数据认证并产生一个tag，在后续加密过程中使用此tag和IV生成校验值U。然后用CTR模式来加密原输入明文数据，在密文的后面附上校验码Ｕ。

GCM：伽罗瓦计数器模式

类似CCM模式，GCM模式是CTR和GHASH的组合，GHASH操作定义为密文结果与密钥以及消息长度在GF（2^128）域上相乘。GCM比CCM的优势是在于更高并行度及更好的性能。TLS 1.2标准使用的就是AES-GCM算法，并且Intel CPU提供了GHASH的硬件加速功能。

分组加密中的填充算法

在分组加密算法中（例如DES），我们首先要将原文进行分组，然后每个分组进行加密，然后组装密文。其中有一步是分组。如何分组？假设我们现在的数据长度是24字节，BlockSize是8字节，那么很容易分成3组，一组8字节，如果现有的待加密数据不是BlockSize的整数倍，那该如何分组？

在分组密码中，有两种常见的填充算法，分别是Pkcs5Padding和Pkcs7Padding。

例如，有一个17字节的数据，BlockSize是8字节，怎么分组？我们可以对原文进行填充（padding），将其填充到8字节的整数倍。假设使用Pkcs5进行填充（以下都是以Pkcs5为示例），BlockSize是8字节（64bit）

待加密数据原长度为1字节：0x41
填充后：0x410x070x070x070x070x070x070x07

待加密数据原长度为2字节：0x410x41
填充后：0x410x410x060x060x060x060x060x06

待加密数据原长度为3字节：0x410x410x41
填充后：0x410x410x410x050x050x050x050x05

待加密数据原长度为4字节：0x410x410x410x41
填充后：0x410x410x410x410x040x040x040x04

待加密数据原长度为5字节：0x410x410x410x410x41
填充后：0x410x410x410x410x410x030x030x03

待加密数据原长度为6字节：0x410x410x410x410x410x41
填充后：0x410x410x410x410x410x410x020x02

待加密数据原长度为7字节：0x410x410x410x410x410x410x41
填充后：0x410x410x410x410x410x410x410x01

待加密数据原长度为8字节：0x410x410x410x410x410x410x410x41
填充后：0x410x410x410x410x410x410x410x410x080x080x080x080x080x080x080x08

PKCS5Padding与PKCS7Padding基本上是可以通用的。在PKCS5Padding中，明确定义Block的大小是8位，而在PKCS7Padding定义中，对于块的大小是不确定的，可以在1-255之间（块长度超出255的尚待研究），填充值的算法都是一样的

pad = k - (l mod k)  //k=块大小，l=数据长度，如果k=8， l=9，则需要填充额外的7个byte的7

可以得出：Pkcs5是Pkcs7的特例（Block的大小始终是8位）。当Block的大小始终是8位的时候，Pkcs5和Pkcs7是一样的。