CBC字节翻转攻击&Padding Oracle Attack原理解析

CBC字节翻转攻击

概述

CBC字节翻转攻击是一种对分组密码的攻击，属于侧信道攻击。这种攻击针对的是CBC Mode，而不是某一种具体的分组密码算法。也就是说，对于分组密码，不论是AES、DES还是3DES，只要分组密码工作在CBC模式下，都适用于字节翻转攻击。CBC字节翻转攻击能够让我们通过修改初始向量iv或密文的值，来控制明文输出。在介绍CBC字节翻转攻击之前，让我们现来了解一下什么是CBC Mode。

CBC Mode简介

CBC 密码分组链接模式（cipher block chaining Triple）。此模式是1976年由IBM所发明，引入了IV初始向量（初始向量：Initialization Vector）的概念。IV是长度为分组大小的一组随机，通常情况下不用保密，不过在大多数情况下，针对同一密钥不应多次使用同一组IV。 CBC要求第一个分组的明文在加密运算前先与IV进行异或；从第二组开始，所有的明文先与前一分组加密后的密文进行异或。

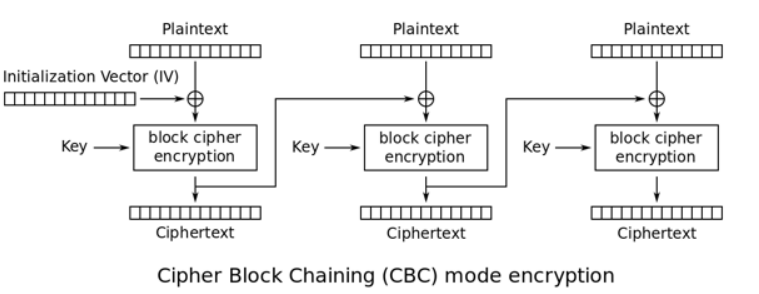
解密过程刚好相反，第一组密文在解密之后与初始向量IV异或得到第一组明文。第二组密文解密之后和第一组密文异或得到第二组明文。也就是说，解密一组明文需要本组和前一组的密文。

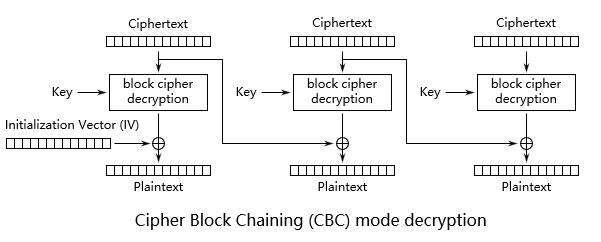
CBC模式相比ECB实现了更好的模式隐藏，但因为其将密文引入运算，加解密操作无法并行操作。同时引入的IV向量，并且还需要加、解密双方共同知晓方可。

CBC字节翻转攻击原理

对于CBC模式的解密算法，每一组明文进行分组算法解密之后，需要和前一组的密文异或才能得到明文。第一组则是和初始向量IV进行异或。

CBC字节翻转攻击的核心原理是通过破坏一个比特的密文来篡改一个比特的明文。

对于异或运算，有以下逻辑：

相同字符之间异或运算的结果为0，即$1 \bigoplus 1=0$

任何字符与0异或运算结果为原字符，即$1 \bigoplus 0=1$

假设现在我们有第$N-1$组密文某一位的值$A$，以及第$N$组密文相同位置经过分组解密后的值$B$，于是我们能够很容易得到第$N$组该位置上的明文$C$

$A \bigoplus B=C$

如果我们破坏第$N-1$组的密文$A$，将其与明文$C$进行异或运算$A \bigoplus C$，由异或的性质可以得到下式

$A \bigoplus C \bigoplus B=C \bigoplus C=0 $

可以看见，现在计算出的明文变成0了，现在我们可以将明文随意更改成我们想要的字符。只需要在上一组的密文异或我们想要的字符即可，假设我们想将明文$C$更改为$X$，可以由下式得出

$A \bigoplus C \bigoplus X \bigoplus B=C \bigoplus C \bigoplus X=X $

此时我们已经通过破坏密文将明文更改成我们想要的字符，具体攻击流程可以参考下图

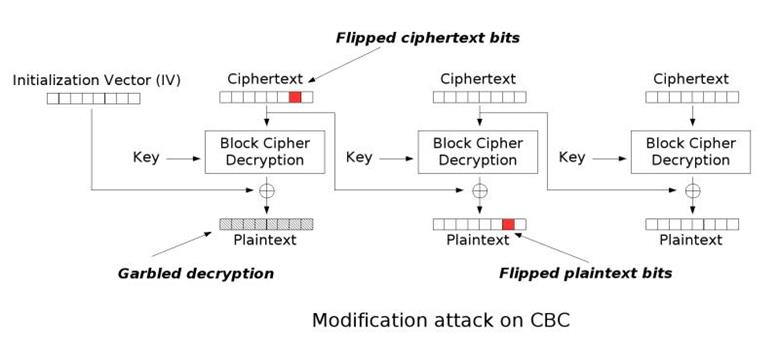
可以使用Python来模拟一下攻击流程

from Crypto.Cipher import AES
import uuid
import binascii


BS=AES.block_size  #分组长度
key=b'test'  #密钥
iv=uuid.uuid4().bytes  #随机初始向量
pad=lambda s: s+((BS-len(s)%BS)*chr(BS-len(s)%BS)).encode()  #Pkcs5Padding
data=b'1234567890abcdefabcdef1234567890'  #明文M

#加密
def enc(data):
    aes=AES.new(pad(key),AES.MODE_CBC,iv)
    ciphertext=aes.encrypt(pad(data))
    ciphertext=binascii.b2a_hex(ciphertext)
    return ciphertext

#解密
def dec(c):
    c=binascii.a2b_hex(c)
    aes=AES.new(pad(key),AES.MODE_CBC,iv)
    data=aes.decrypt(c)
    return data

#测试CBC翻转
def CBC_test(c):
    c=bytearray(binascii.a2b_hex(c))
    c[0]=c[0]^ord('a')^ord('A') #c[0]为第一组的密文字符，a为第二组相应位置的明文字符，A是我们想要的明文字符
    c=binascii.b2a_hex(c)
    return c

print("ciphertext:",enc(data))
print("data:",dec(enc(data)))
print("CBC Attack:",dec(CBC_test(enc(data))))

运行结果

ciphertext: b'ffa645d1b5e40afbbae47de053a66f978fa0a824e99864a7e8baf38ceccda613c304883f11fc0857c1bb7603f859798e'
data: b'1234567890abcdefabcdef1234567890\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'
CBC Attack: b':8O<\xe7\x04\xd8v\xe8Q\xfe\xa5I\xc9c]Abcdef1234567890\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'

可以看到第二组密文解密之后已经被我们更改成了A，而由于我们更改了第一组的密文，所以第一组解密的明文变成了乱码。如果我们想要更改第一组的明文，则需要修改初始向量IV的值。

通过CBC字节翻转攻击，假如我们能够触发加解密过程，并且能够获得每次加密后的密文。那么我们就能够在不知道key的情况下，通过修改密文或IV，来控制输出明文为自己想要的内容，而且只能从最后一组开始修改，并且每改完一组，都需要重新获取一次解密后的数据，要根据解密后的数据来修改前一组密文的值。

Padding Oracle Attack

概述

填充提示攻击（ Padding Oracle Attack ），Padding的含义是“填充”，在解密时，如果算法发现解密后得到的结果，它的填充方式不符合规则，那么表示输入数据有问题，对于解密的类库来说，往往便会抛出一个异常，提示Padding不正确。Oracle在这里便是“提示”的意思，并不是我们常说的甲骨文公司。

Padding Oracle Attack针对的同样是CBC模式下的分组密码，如果满足攻击条件，那么利用Padding Oracle能够在不知道密钥的情况下，解密任意密文，或者构造出任意明文的合法密文。

Padding Oracle Attack的利用条件

攻击者能够获得密文，以及密文对应的初始化向量iv
攻击者能够触发密文的解密过程，并且能够知道密文的解密结果是否正确

密码学里的iv，并没有保密性的要求，所以对于使用CBC Mode的加密算法来说，iv经常会随着密文一起发送。常见的做法是将iv作为一个前缀，附着在密文的前面。对于CBC Mode来说，iv的长度必须与分组的长度相等。

在介绍 Padding Oracle Attack 之前，让我们先了解一下分组密码中常见的填充算法。

分组密码中常见的填充算法

在分组加密算法中（例如DES），我们首先要将原文进行分组，然后每个分组进行加密，然后组装密文。其中有一步是分组。如何分组？假设我们现在的数据长度是24字节，BlockSize是8字节，那么很容易分成3组，一组8字节，如果现有的待加密数据不是BlockSize的整数倍，那该如何分组？

在分组密码中，有两种常见的填充算法，分别是Pkcs5Padding和Pkcs7Padding。

例如，有一个17字节的数据，BlockSize是8字节，怎么分组？我们可以对原文进行填充（padding），将其填充到8字节的整数倍。假设使用Pkcs5进行填充（以下都是以Pkcs5为示例），BlockSize是8字节（64bit）

待加密数据原长度为1字节：0x41
填充后：0x410x070x070x070x070x070x070x07

待加密数据原长度为2字节：0x410x41
填充后：0x410x410x060x060x060x060x060x06

待加密数据原长度为3字节：0x410x410x41
填充后：0x410x410x410x050x050x050x050x05

待加密数据原长度为4字节：0x410x410x410x41
填充后：0x410x410x410x410x040x040x040x04

待加密数据原长度为5字节：0x410x410x410x410x41
填充后：0x410x410x410x410x410x030x030x03

待加密数据原长度为6字节：0x410x410x410x410x410x41
填充后：0x410x410x410x410x410x410x020x02

待加密数据原长度为7字节：0x410x410x410x410x410x410x41
填充后：0x410x410x410x410x410x410x410x01

待加密数据原长度为8字节：0x410x410x410x410x410x410x410x41
填充后：0x410x410x410x410x410x410x410x410x080x080x080x080x080x080x080x08

PKCS5Padding与PKCS7Padding基本上是可以通用的。在PKCS5Padding中，明确定义Block的大小是8位，而在PKCS7Padding定义中，对于块的大小是不确定的，可以在1-255之间（块长度超出255的尚待研究），填充值的算法都是一样的

pad = k - (l mod k)  //k=块大小，l=数据长度，如果k=8， l=9，则需要填充额外的7个byte的7

可以得出：Pkcs5是Pkcs7的特例（Block的大小始终是8位）。当Block的大小始终是8位的时候，Pkcs5和Pkcs7是一样的。

注意

当待填充的序列恰好为8个字节时，仍需要在尾部填充8个字节的0x08，这可以让解密的数据准确无误地移除多余字节。

Padding Oracle流程

我们首先来考虑一个具体的场景：

某程序使用Cookie来加密传递用户的加密用户名、公司 ID 和角色 ID。该Cookie使用CBC Mode加密，每个Cookie使用一个唯一的初始化向量iv，该向量位于密文之前。

当应用程序收到一个加密Cookie时，它有以下三种响应方式：

当收到一个有效的密文（一个被正确填充并包含有效数据的密文）时，应用程序正常响应（200 OK）
当收到无效的密文时（解密时填充错误的密文），应用程序会抛出加密异常（500 内部服务器错误）
当收到一个有效密文（解密时正确填充的密文）但解密为无效值时，应用程序会显示自定义错误消息 (200 OK)

上面描述的场景是一个经典的Padding Oracle，因为我们可以使用程序的行为来确定提供的加密值是否被正确填充。术语Oracle是指可用于确定测试是否成功或失败的提示。

假设有一个员工，其信息分别为：用户名：BRIAN、公司ID：12、角色ID：1。各信息之间用分号分隔，于是可以表示成以下形式：BRIAN;12;1;

假如我们使用Pkcs5填充，可以将其转换成以下形式

BRIAN;12;1;0x050x050x050x050x05
#16字节，符合Pkcs5分组长度，可以将以上字符串分为两组，每组8字节

下面是CBC的加密过程

https://s3.amazonaws.com/s3.media.squarespace.com/production/936190/11268292/l/po_fig3.png — CBC加密

这里设置的初始向量iv为0x7B 0x21 0x6A 0x63 0x49 0x51 0x17 0x0F，这时服务器发送的Cookie应该为7B216A634951170FF851D6CC68FC9537858795A28ED4AAC6，初始向量iv被填充在加密密文之前。

CBC解密过程如下

https://s3.amazonaws.com/s3.media.squarespace.com/production/936190/11268292/l/po_fig4.png — CBC解密

密文进行分组解密之后会产生中间值Intermediary Value，这些中间值再和前一组密文异或便会得到本组明文。解密出的明文后面会有正确的填充块。当然在客户端，我们无法得知这些中间值是什么。

Padding Oracle 解密漏洞利用

根据服务端发送的Cookie，我们能够获得加密的初始向量iv以及密文。那么我们该如何利用Padding Oracle Attack呢？

利用测试一

首先我们可以更改Cookie 中的初始向量iv，将iv的值改为全零，并且只发送第一个加密块。此时Cookie变为

Cookie：0000000000000000F851D6CC68FC9537

服务器端的解密过程如下

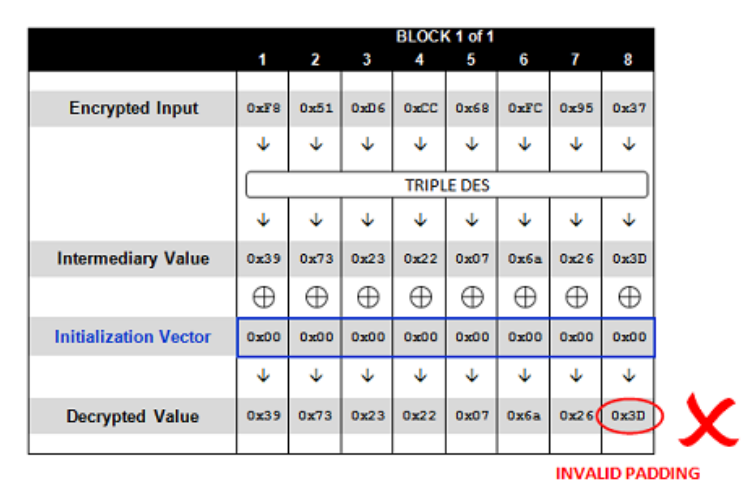
可以看到，如果按照我们发送的错误数据来解密的话，最后一位数据是0x3D。而正常的解密数据最后是包含填充数据的。对于分组长度为8字节来说，这些填充数据的值位于0x01-0x08，而0x3D并不在其中。所以服务器会检测到填充块错误，返回500异常。

利用测试二

我们再次更改Cookie中的初始向量iv，和上次不同的是，我们将iv最后一位的值改为0x01，此时Cookie的值如下

Cookie：0000000000000001F851D6CC68FC9537

我们再次将Cookie发送给服务器端解密

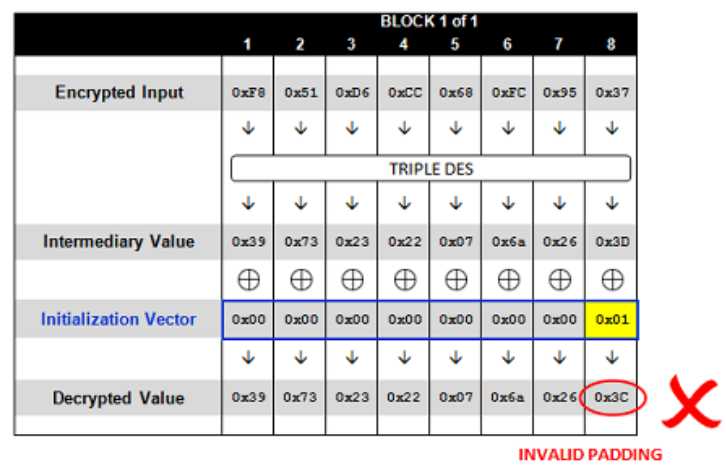
可以看见，此时明文最后一位变成了0x3C，这仍然不是正确的填充数据，服务器同样会返回500异常。但是与上次不一样的是，明文最后一位的值从0x3D变为了0x3C。也就是说，我们可以通过控制初始向量iv的值来控制明文输出。

如果我们重复发出相同的请求并每次只更改iv中同一个字节的值（最多至0xFF），我们肯定能够碰到一个值，使明文符合填充规律。

利用测试三

假设我们通过不断发送类似的Cookie给服务器端解密，找到了一个使明文符合填充规律的Cookie，此时服务器端的解密过程如下

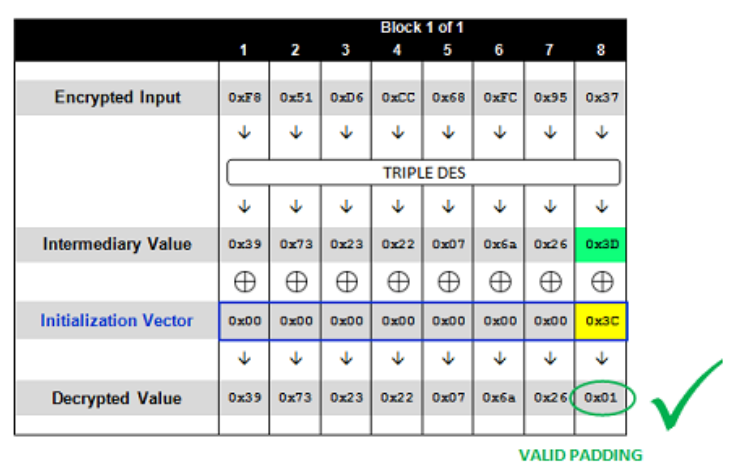
解密后的明文最后一位为0x01，符合填充规律，但是明文结果并不正确。此时服务器会返回200OK自定义页面。由于填充规律是固定的，我们只更改了一位iv的值，所以解密明文肯定是一位填充数据，值为0x01。此时我们可以根据以下公式得到一位加密的中间值0x3D

$0x3D=0x3C \bigoplus 0x01$

利用测试四

类似地，我们可以爆破iv值的每一位，直到解密出来的每一位明文数据都变成全部符合填充规律的0x08，解密过程如下

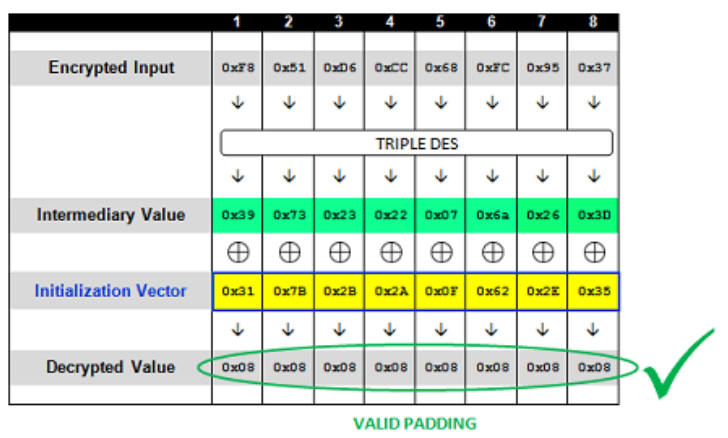
至此，我们可以利用Padding Oracle Attack来爆破出每一组加密中间值。然后再使用第一组的中间值和服务器端初始的iv异或，便可以得到第一组明文$m$。继续使用CBC Mode解密，可以依次得到所有明文分组。

对于每一组，至多需要尝试256*8次也就是2048次，便可爆破出加密中间值。这样我们就可以绕过加密，从而直接获得密文的明文。这种攻击手法类似于sql注入中的布尔盲注，通过服务器端不同的回显作为布尔条件，从而判断构造的数据是否正确，进而爆破出所有正确的结果。

利用测试五

在利用测试四中，我们已经能够利用Padding Oracle Attack爆破出所有中间值和明文了，那么我们该怎么构造出任意明文的合法密文呢？

首先我们先看单一分组的情况

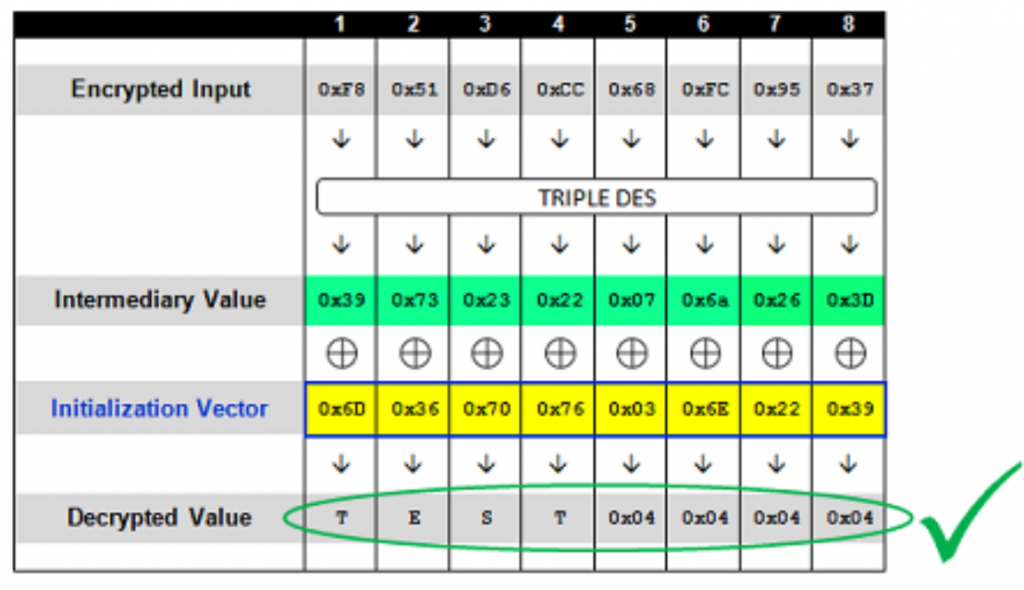
由于我们已经爆破出了intermediary，所以我们可以很容易地构造出iv来生成任意明文。

那么对于多组明文，情况又是怎样的呢？

先从最后一组开始，爆破最后一组的intermediary并构造出iv，然后将本组的iv当作前一组的密文，以此类推。由此我们可以得到构造密文的步骤

从最后一组开始，爆破出该组的intermediary并构造出iv，然后将本组的iv当作前一组的密文
爆破前一组的intermediary并构造出iv，然后将本组的iv当作前一组的密文
…
最后会得到第一组的iv，至此我们已经构造出了所有合法密文以及iv

参考文章