前言

最近在WMCTF中碰到了一道对抗样本相关的CTF题目——easynum，而对于对抗样本攻击我一直还停留在论文层面，因此觉得雪殇出的这道题目是个不错的小demo，可以实践学习一下。

什么是对抗样本攻击

简单来说，就是指向干净样本（clean example）中添加微小的不易察觉的扰动生成对抗样本（adversarial example），若将生成的对抗样本输入深度神经网络，神经网络会以较高的概率输出错误的分类结果。

如上图，基于熊猫图像，攻击者向原始图像添加了微小的扰动（失真），这导致模型以较高的置信度将该图像标记为长臂猿。

根据生成特征的不同,可以将对抗攻击方法分为如下几类

1. 基于梯度的攻击方法
   • 利用干净样本的梯度信息生成对抗样本
2. 基于优化的攻击方法
   • 利用优化目标函数生成对抗样本
3. 基于转移的攻击方法
   • 利用对抗攻击之间的转移性生成对抗样本
4. 基于GAN的攻击方法
   • 利用 GAN网络生成深度神经网络难以区分的对抗样本
5. 基于决策边界的攻击方法
   • 利用差分进化算法,以迭代的方式生成最佳的对抗样本

而本题目使用到的快速梯度符号法（FGSM）就是一种基于梯度的攻击方法。

easynum

题目给了源码和模型文件，其中源码inference.py如下

import socket
import tensorflow as tf
import numpy as np


model = tf.keras.models.load_model('model.h5')

def predict(input_data):
    processed_data = np.array(input_data).reshape(1, 20, 1) 
    prediction = model.predict(processed_data)

    if prediction[0][0] > 0.99 and np.mean(input_data) > 0.5:
        return "FLAG{}"
    
    return f"模型预测输出: {prediction[0][0]}"

def start_server(host='0.0.0.0', port=12345):
    server_socket = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
    server_socket.bind((host, port))
    server_socket.listen(1)
    print(f"服务器正在 {host}:{port} 等待连接...")

    while True:
        client_socket, addr = server_socket.accept()
        print(f"连接来自: {addr}")
        client_socket.sendall(b"welcome\n")

        while True:
            data = client_socket.recv(1024)
            if not data:
                break

            # 处理输入数据
            input_values = list(map(float, data.decode('utf-8').strip().split()))
            if len(input_values) != 20:
                client_socket.sendall("wong\n")
                continue

            response = predict(input_values)
            client_socket.sendall(response.encode('utf-8') + b'\n')

        client_socket.close()

if __name__ == "__main__":
    print(predict(input_value))

其中核心逻辑如下

def predict(input_data):
    processed_data = np.array(input_data).reshape(1, 20, 1) 
    prediction = model.predict(processed_data)

    if prediction[0][0] > 0.99 and np.mean(input_data) > 0.5:
        return "FLAG{}"
    
    return f"模型预测输出: {prediction[0][0]}"

当输入的推理结果大于0.99且输入的均值大于0.5时，输出flag。对抗样本的思想是向输入添加微小扰动来最大化损失函数，我们当然也可以取反扰动符号来最小化损失，使预测精度大于0.99。因此题目的思路就是生成一个随机张量作为干净样本，然后向其添加对抗扰动，来使对抗样本的预测精度上升。

下面的问题就是如何生成对抗扰动，这里选择最经典的扰动生成算法快速梯度符号法（Fast Gradient Sign Method，FGSM）

FGSM

FGSM是一种白盒攻击，其基本原理是使用模型的损失函数对输入数据求梯度（具体来说是梯度的符号），然后在输入数据上加上一个与损失函数梯度方向相同的扰动，使模型在预测时产生最大的分类误差，来干扰模型的预测结果

$x_{\mathrm{adv}}=x+\epsilon*\mathrm{sign}(\nabla_xJ(\theta,x,y))$

其中$x$是原始输入样本，$adv_x$是生成的对抗样本，$\nabla_xJ(\theta,x,y)$表示损失函数相对于输入x的梯度（$\theta$代表模型参数，$y$代表原始输入标签），$\mathrm{sign}$是符号函数，$\epsilon$是扰动系数，用于控制扰动幅度。

由于对抗样本攻击的目标是降低模型预测精度，因此扰动的方向和模型梯度方向相同，可以理解成一种梯度上升算法（对比于训练过程中的梯度下降算法SGD，参数更新方向是梯度的反方向）。而对于本题来说，我们想让对抗样本的预测精度上升并大于$0.99$，这可以看作是一种目标攻击，因此对抗样本的生成可以写成如下形式

$x_{\mathrm{adv}}=x\textcolor{red}{-}\epsilon*\mathrm{sign}(\nabla_xJ(\theta,x,y))$

解题过程

根据上述思路，可以写出如下扰动生成代码

import tensorflow as tf
import numpy as np


def FGSM_perturbation(model, input_data, epsilon=0.1):
    input_tensor = tf.convert_to_tensor(input_data.reshape(1, 20, 1), dtype=tf.float32)
    with tf.GradientTape() as tape:
        tape.watch(input_tensor)
        # 预测结果
        prediction = model(input_tensor)

        #标签设置为1
        true_label = tf.convert_to_tensor([[1]], dtype=tf.float32)  # Shape: (1, 1)
        #计算输入损失
        loss = tf.keras.losses.binary_crossentropy(true_label, prediction)
    #反向传播计算损失函数相对输入的梯度
    gradient = tape.gradient(loss, input_tensor)

    if gradient is None:
        raise ValueError("梯度计算失败，gradient 为 None")

    # 生成对抗样本，注意这里的符号是梯度方向还是梯度的反方向，添加梯度方向的扰动会最大化损失函数，造成精度下降，反之会导致精度上升
    adversarial_input = input_tensor - epsilon * tf.sign(gradient)
    #归一化
    adversarial_input = tf.clip_by_value(adversarial_input, 0, 1)  # 确保值在有效范围内
    return adversarial_input.numpy().reshape(20)

下面开始生成样本

def find_flag(model, attempts=5):
    for _ in range(attempts):
        #随机生成输入
        base_input = np.random.rand(20)
        prediction = model.predict(base_input.reshape(1, 20, 1))
        print("扰动前精度:", prediction)
        adversarial_input = FGSM_perturbation(model, base_input)
        prediction = model.predict(adversarial_input.reshape(1, 20, 1))
        print("扰动后精度:", prediction)
        print("---------------------------------------")
        print("均值:", np.mean(adversarial_input))
        if prediction[0][0] > 0.99 and np.mean(adversarial_input) > 0.5:
            print(f"找到的对抗输入: {adversarial_input}")
            return adversarial_input  # 找到有效输入时返回

    print("未找到有效的对抗输入")
    return None  # 如果没有找到有效输入，返回 None

可以看到向随机生成的样本添加$\epsilon=0.1$的最小化损失函数对抗扰动后，模型的预测精度上升很快，基本一次就能得到所需的对抗样本

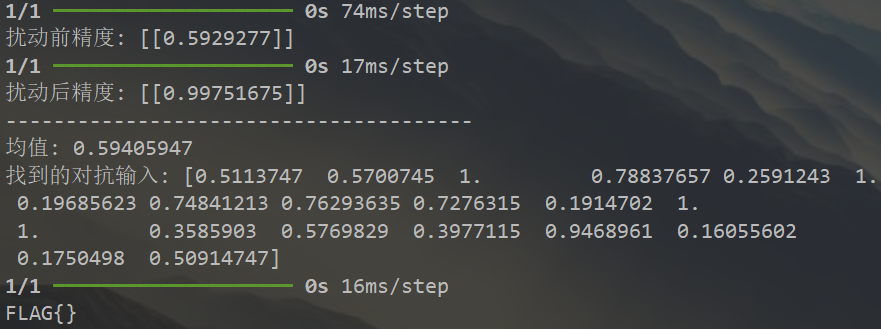
非预期解

盲猜20个1居然出了

当然，如果运气没这么好，古法爆破也是可以的，随机生成20个$[0,1]$的浮点数很快也能爆出flag。