梯度下降算法(Gradient Descent Algorithm)
梯度下降算法是机器学习领域最常见的目标优化算法之一:目标损失函数$\ell(\theta)$关于参数$\theta$的梯度是损失函数上升最快的方向,而我们的目标是最小化损失函数$\ell(\theta)$,因此需要将参数沿着梯度相反的方向前进一个步长$\eta$,就可以实现损失函数的下降,其中$\eta$又称为学习率。梯度下降算法的更新过程如下
$\theta \leftarrow \theta-\eta\cdot\nabla\ell(\theta)$
对于无约束的单目标优化问题$\min f(x)$,能够利用梯度下降算法进行优化:$x_{k+1}=x_k+\alpha_kd_k$,其中$\alpha_k$为步长,$d_k$为更新方向。当$d_k=-\nabla f(x_k)$时,即为标准的梯度下降算法,也叫最速下降算法。证明如下:
首先对$f(x_{k+1})$进行泰勒展开
$f(x_{k+1})=f(x_k+\alpha_kd_k)=f(x_k)+\alpha_k\nabla f(x_k)^Td_k+O(\alpha_k),\;\alpha_k>0$
则目标函数沿着$d_k$方向更新的速率为
$\lim_{\alpha_k\to0}\frac{f(x_k+\alpha_kd_k)-f(x_k)}{\alpha_k}=\lim_{\alpha_k\to0}\frac{\alpha_k\nabla f(x_k)^Td_k+O(\alpha_k)}{\alpha_k}=\nabla f(x_k)^Td_k=||\nabla f(x_k)||\cdot||d_k||\cos\theta$
其中$\theta$为梯度$\nabla f(x_k)$与更新方向$d_k$之间的夹角,若要使函数$f(x_k)$沿着$d_k$下降(即$f(x_k+\alpha_kd_k)<f(x_k)$),则有$\theta>90\degree$;要使得下降速率最大,则夹角$\theta=180\degree$,即更新方向$d_k$为梯度的反方向$-\nabla f(x_k)$。此时$d_k$可以表示成如下优化
$d_k=\arg\min_d\;\{\nabla f(x_k)^Td+\frac 12||d||^2\}$
上述优化目标同时对$d$的方向和大小进行优化,保证更新方向$d$能够有效减少目标函数值的同时,控制$d$的大小。其中$\frac 12||d||^2$为正则项,确保更新方向$d$不会过大,从而避免更新步长过大导致的不稳定性。
该优化问题的解可以令导数为零来求解,即
$\nabla f(x_k)+d=0\Longrightarrow d=-\nabla f(x_k)$
多重梯度下降问题描述
上面可以看出,梯度下降的本质其实是找到一个搜索方向$d_k$,使得目标函数沿着$d_k$的更新速率为负$\nabla f(x_k)^Td_k<0$。那么对于$m$多目标问题,如果能找到一个搜索方向$d_k$,使得$\nabla f_i(x_k)^Td_k<0,\;\forall i\in m$,则该方向会使得所有目标函数都沿下降的方向更新。
类似单目标梯度下降,多目标梯度下降方向的求解,可以表示为下面一个最小-最大优化问题
$d_k=\arg\min_d\;\{\max_i\nabla f_i(x_k)^Td+\frac{1}{2}||d||^2\}\qquad (1)$
这个问题的目标是找到一个搜索方向$d_k$,使得在所有目标函数的更新速率$\nabla f_i(x_k)^Td$中,连最大的那个更新速率值都尽可能小。
但式$(1)$并不好直接求解,我们可以将其改写为如下形式的约束优化问题
$\begin{cases}(d_k,\alpha_k)=\min\{\alpha+\frac{1}{2}||d||^2\}\\ s.t.\quad\nabla f_i(x_k)^Td\leq\alpha,\;\;\forall i\in m&\end{cases}\qquad (2)$
$(2)$式中引入了一个辅助变量$\alpha=\max_i\nabla f_i(x_k)^Td$,将最大化问题转化为一个不等式约束条件$\nabla f_i(x_k)^Td\leq\alpha$。通过引入辅助变量$\alpha$和约束条件,我们将原始的最大化-最小化问题转化为一个带有约束的优化问题,因此下面可以通过一些标准的优化算法如拉格朗日乘数法、KKT条件等来求解上述的约束优化问题。
优化理论基础
拉格朗日乘数法
拉格朗日乘数法是一种用于求解约束优化问题的数学方法。它通过引入拉格朗日函数,将约束条件与目标函数结合,从而将约束优化问题转化为无约束优化问题。
假设有如下优化问题,想要求目标函数的最小值
$\begin{aligned}&\min\quad f_{0}(x),x\in\mathbb{R}^{n}\\&s.t.\quad f_{i}\left(x\right)\leq0,\text{其中i}=1,2,3\ldots\mathrm{m}\end{aligned}$
则该问题的拉格朗日函数可以写为如下形式,其中$\lambda_i$称作拉格朗日乘子
$L(x,\lambda)=f_0(x)+\sum\lambda_if_i(x)$
然后我们可以通过求解该函数的极值点来找到原问题的解。下面给出一个直观的例子
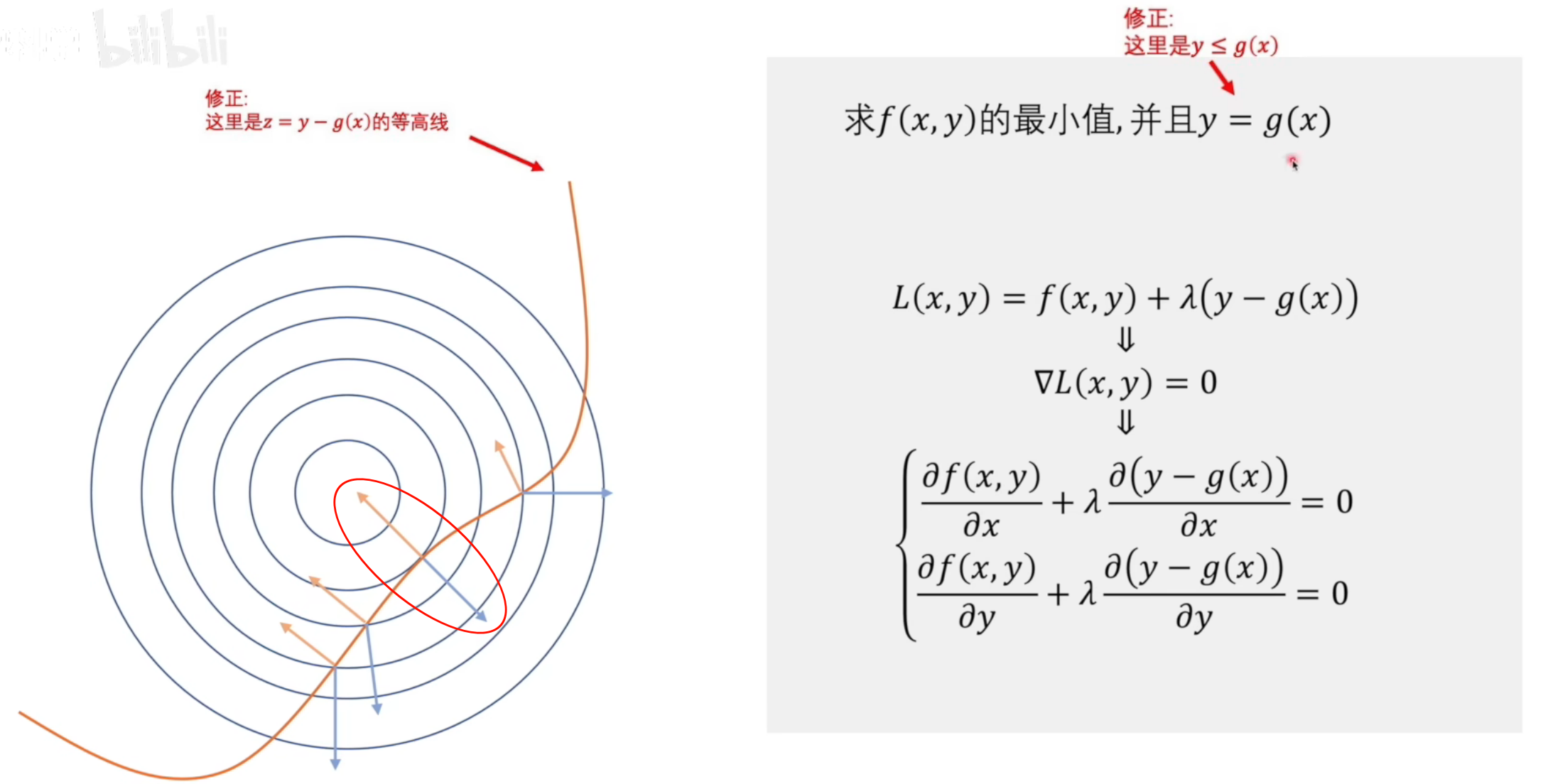
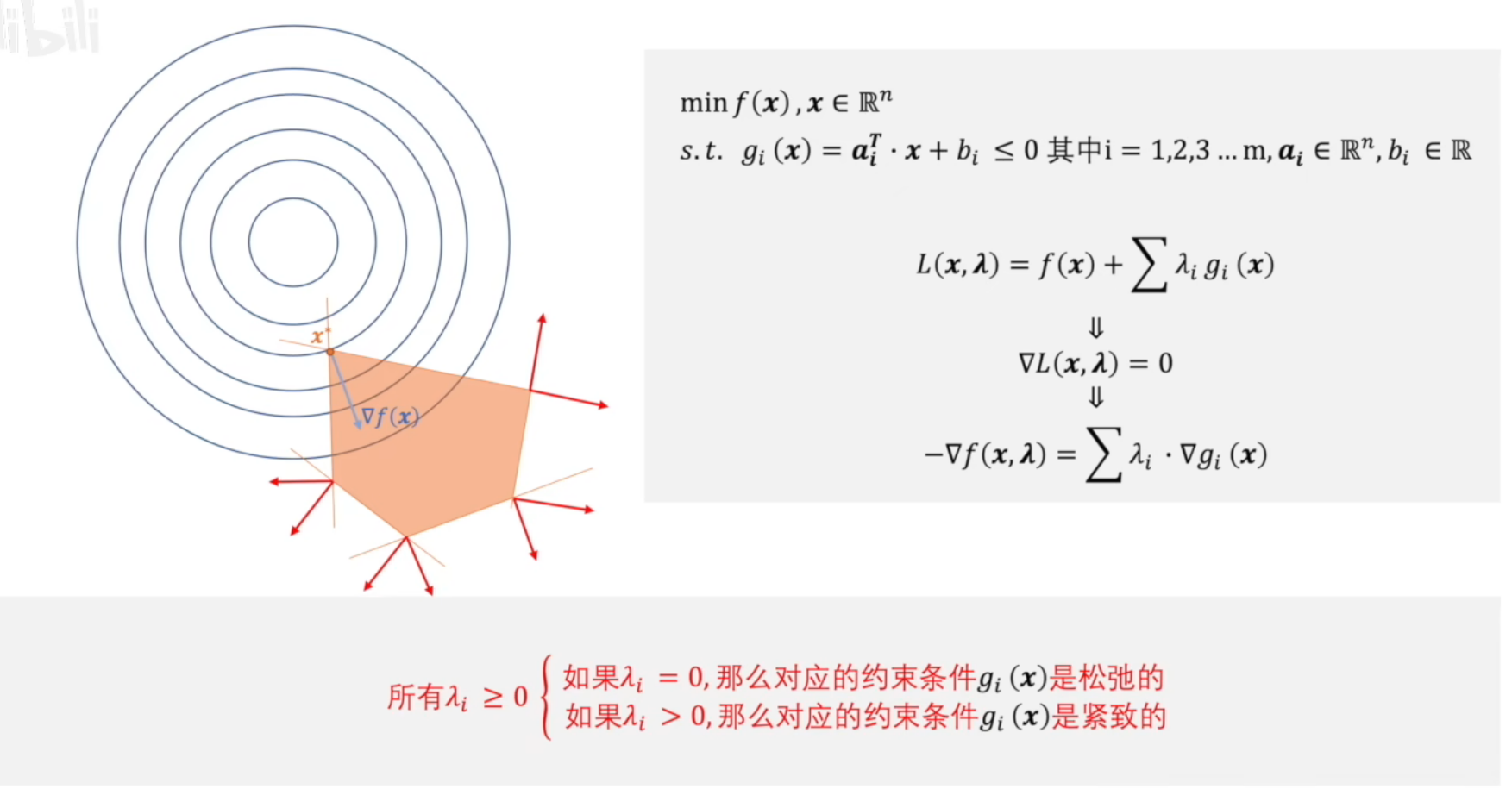
蓝线代表目标函数,黄线代表约束条件,则上图红圈中的相切点即为所求约束问题的最小值。在切点处有$\nabla L(x,y)=0$,这是因为在切点处目标函数和约束函数的梯度方向一致,通过控制拉格朗日算子$\lambda$的大小,即可得到$\nabla L(x,y)=0$。因此由$\nabla L(x,y)=0$求解拉格朗日函数的极值极为原约束问题的解。上面是一个二元单约束条件的情况,下面是一个更复杂的多元多约束条件的情况。
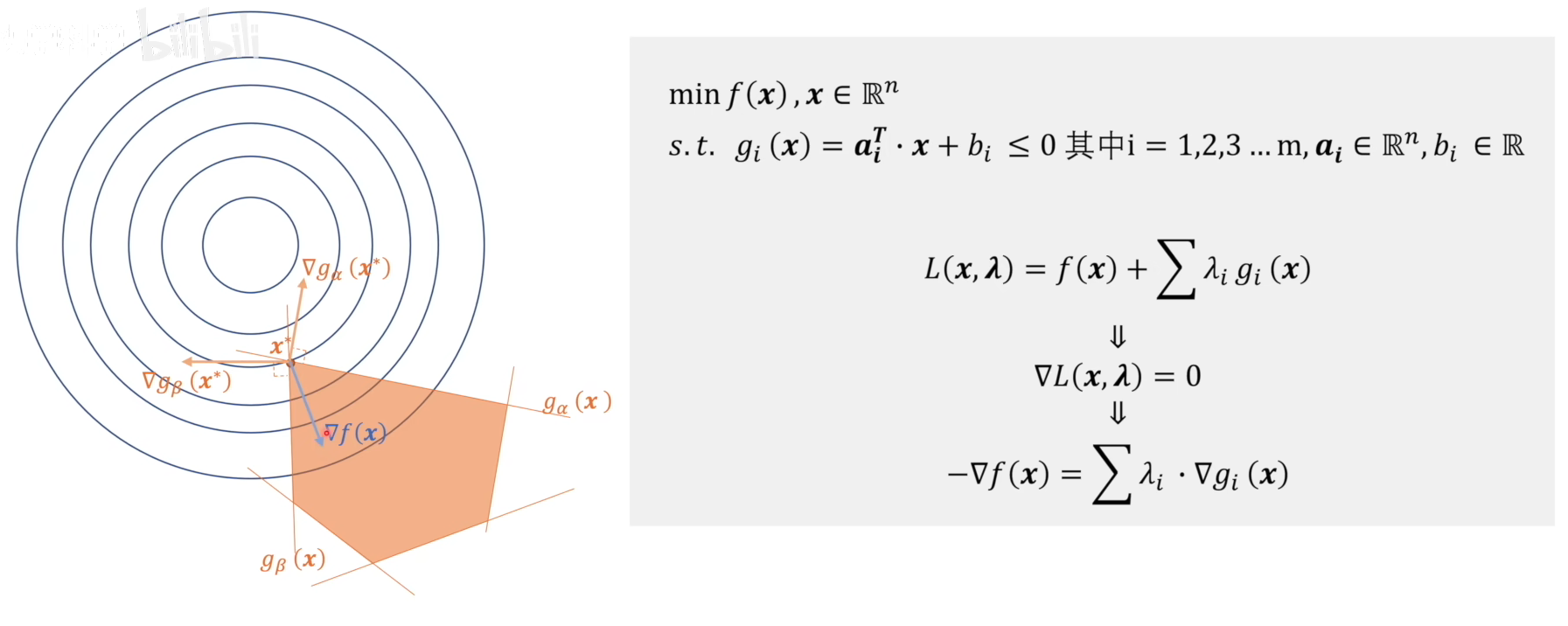
该约束问题的解在图中表示为$x^*$,为了简化,图中只给出了$5$个约束条件。在极值点$x=x^*$处有
$\begin{aligned}&g_{\alpha}\left(x^{*}\right)=g_{\beta}\left(x^{*}\right)=0(边界条件)\\&\lambda_{\alpha}\nabla g_{\alpha}\left(x^{*}\right)+\lambda_{\beta}\nabla g_{\beta}\left(x^{*}\right)=-\nabla f\left(x\right)\Longrightarrow\lambda_{\alpha},\lambda_{\beta}\neq0(保证拉格朗日函数梯度为0)\end{aligned}$
而对于其他三个约束条件,有
$\begin{aligned}&\text{其他}g_i\left(x^*\right)<0,\\&\lambda_{i}\cdot\nabla g_{i}\left(x\right)=0\Rightarrow\lambda_{i}=0\left(i\neq\alpha,\beta\right)(保证拉格朗日函数梯度为0)\end{aligned}$
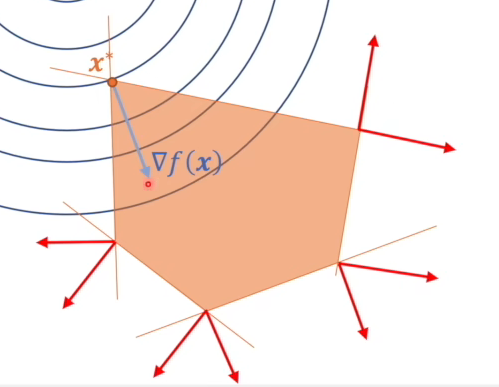
从图中可以看到,其他三个约束条件的梯度对$\nabla f(x)$实际上是没有起到约束作用的,因此可以得到下面一个结论
所有$\lambda_i\ge0$,$\begin{cases}如果\lambda_i=0,那么对应的约束条件g_i(x)是松弛的(不起作用的约束条件)\\ 如果\lambda_i>0,那么对应的约束条件g_i(x)是紧致的(起作用的约束条件)&\end{cases}$
还有下面一种特殊情况,即目标函数最小值$x=x^*$位于可行域之内,这种情况就相当于整个可行域都是松弛的,可以直接转换为无约束问题。

上述是拉格朗日乘数法几个较为直观的例子,然而拉格朗日乘数法存在一个问题,即拉格朗日函数求得的极值不一定是原目标函数的最值。这就引出了凸问题的概念。
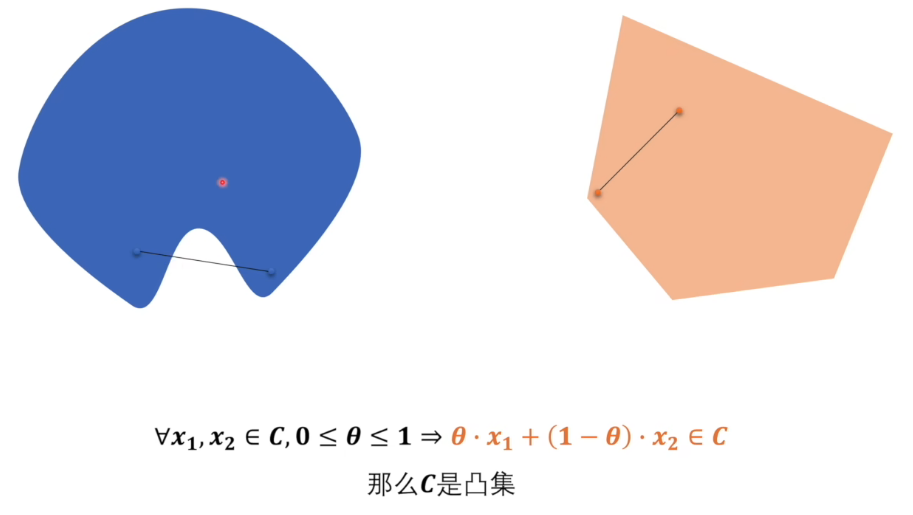
凸集
一个集合$C\subseteq\mathbb{R}^n$是凸集,如果对于集合中的任意两点$x_1,x_2\in C$和任意$\lambda\in[0,1]$,它们的凸组合仍然属于$C$,即:
$\lambda x_1+(1-\lambda)x_2\in C,\quad\forall x_1,x_2\in C,\lambda\in[0,1]$
下面是一些常见的凸集
- 欧几里得空间
- 整个空间$\mathbb{R}^{n}$是凸集
- 超平面
- 超平面$\{x\in\mathbb{R}^n\mid a^\top x=b\}$是凸集
- 半空间
- 半空间$\{x\in\mathbb{R}^n\mid a^\top x\le b\}$是凸集
- 多面体
- 多面体$\{x\in\mathbb{R}^n\mid Ax\leq b\}$是凸集
- 单纯形
- 在几何学中,单纯形是最简单的多面体,由$n+1$个顶点在$n$维空间中的凸包构成,如
- $0$-单纯形——点($0$维$1$点)、$1$-单纯形——线段($1$维$2$点)、$2$-单纯形——三角形($2$维$3$点)
- $n$-单纯形——$n$维空间中的超多面体,由$n+1$个顶点构成
之所以首先介绍凸集,是因为凸集有一些良好的性质
- 凸集的交集仍然是凸集
- 如果$C_1$和$C_2$是凸集,那么$C_1\cap C_2$也是凸集
- 这一性质可以推广到任意多个凸集的交集
- 凸集的仿射变换仍然是凸集
- 果$C$是凸集,$A$是矩阵,$b$是向量,则集合$\{Ax+b\mid x\in C\}$也是凸集
- 凸集的和集也是凸集
- 如果$C_1$ 和$C_2$是凸集,那么它们的和集$C_1+C_2=\{x_1+x_2\mid x_1\in C_1,x_2\in C_2\}$也是凸集。
- 凸包的凸性
- 任意集合的凸包(包含该集合的最小凸集)是凸集
凸包
给定一组点$P=\{p_1,p_2,\ldots,p_n\}$,凸包是包含所有这些点的最小凸集。在二维情况下,凸包是一个凸多边形,其顶点是$P$中的某些点,。在三维情况下,凸包是一个凸多面体。
凸包有以下性质
- 最小性:凸包是包含所有点的最小凸集,即不存在比凸包更小的凸集能够包含所有点。
- 唯一性:给定一组点,其凸包是唯一的。
- 边界:凸包的边界由点集中的某些点组成,这些点称为凸包的顶点。
凸组合
给定一组点$x_1,x_2,\ldots,x_n$和一组权重$\lambda_1,\lambda_2,\ldots,\lambda_n$,凸组合定义为
$\begin{aligned}&y=\sum_{i=1}^n\lambda_ix_i\\&s.t.\;\lambda_i\geq0\;\,\sum_{i=1}^n\lambda_i=1\end{aligned}$
点$x_i$可以是向量、标量或其他数学对象。凸组合的几何意义是点的加权平均,其中权重决定了每个点在组合中的贡献。凸组合的结果$y$位于点$x_1,x_2,\ldots,x_n$的凸包内。如果所有点$x_i$属于一个凸集,那么它们的凸组合$y$也属于该凸集。
单纯形
在数学中,单纯形可以通过凸组合来定义。给定$n+1$个仿射独立的点$v_0,v_1,\ldots,v_n$,单纯形$S$定义为这些点的凸组合
$\begin{aligned}S=\left\{\sum_{i=0}^n\lambda_iv_i\middle |\lambda_i\geq0,\sum_{i=0}^n\lambda_i=1\right\}\end{aligned}$
其中$\lambda_i$是权重系数,表示每个顶点在单纯形中的贡献。单纯形的维度由顶点的数量决定。
单纯形在优化中最重要的应用是单纯形法(Simplex Method),单纯形法是一种迭代算法用于求解线性规划问题
$\begin{aligned}&\max c^\top x\\&s.t.\;Ax\le b,\;x\ge0\end{aligned}$
单纯形法的核心思想是
- 线性规划问题的可行域是一个凸多面体(单纯形的推广)
- 最优解一定出现在可行域的顶点(单纯形的顶点)上
- 线性函数的性质决定了其极值(最大值或最小值)一定出现在可行域的边界上,而不是内部
- 如果可行域是一个凸多面体,极值一定出现在顶点上
- 单纯形法通过从一个顶点移动到相邻顶点,逐步逼近最优解
单纯形法的算法流程如下
- 初始化:找到一个初始可行解(顶点)
- 迭代:
- 检查当前顶点是否是最优解
- 如果不是,选择一个相邻顶点,使得目标函数值增加
- 终止:当找到最优解或确定问题无界时,停止迭代
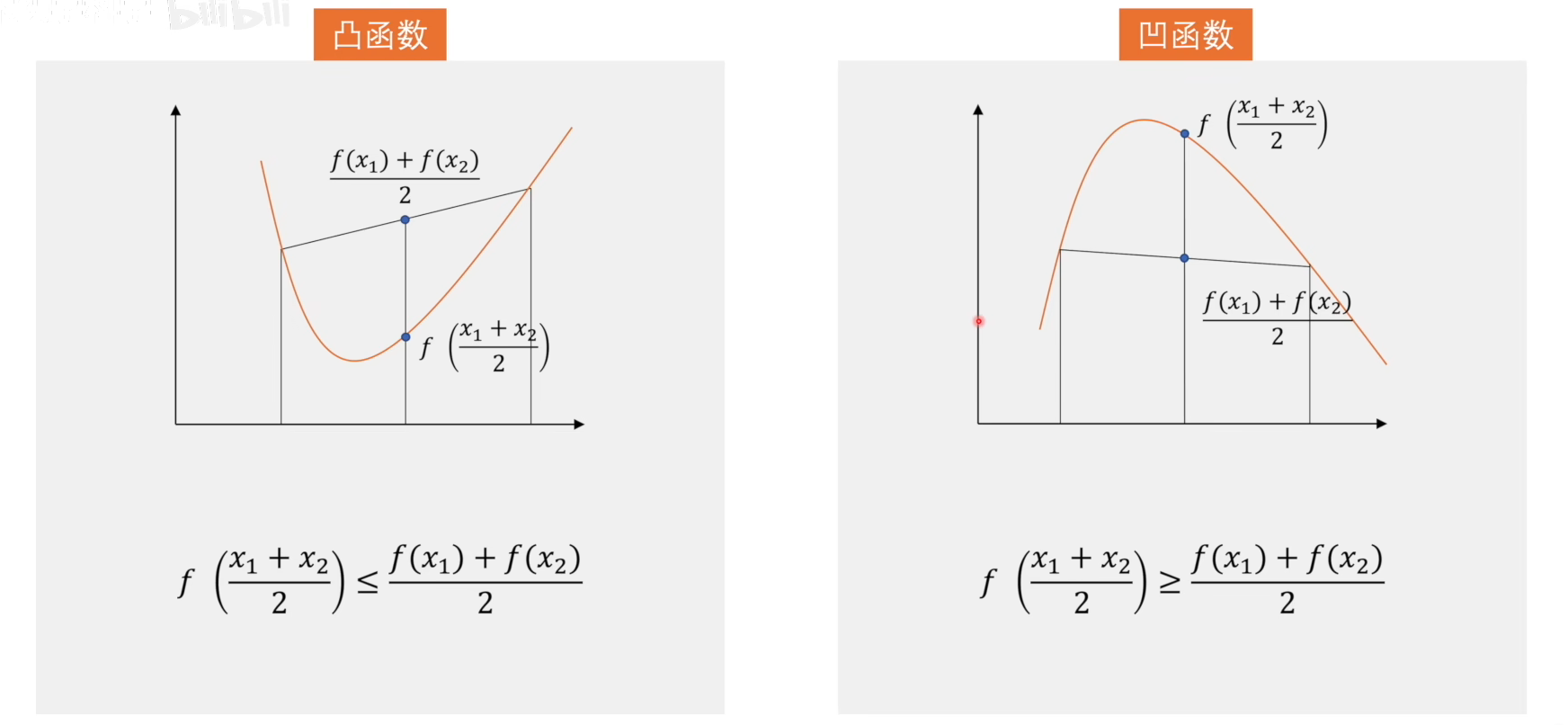
凸函数
在机器学习中,凸函数是一类非常重要的函数,因为它们在优化问题中具有良好的性质,能够保证找到的局部最优解就是全局最优解。在优化理论中,与凸函数相对的为非凸函数。而在数学中,与凸函数相对的是凹函数。
一个函数$f:\mathbb{R}^n\to\mathbb{R}$是凸函数,如果对于定义域内的任意两点$x_1,x_2$和任意$\lambda\in[0,1]$,满足以下不等式。如果不等式是严格的(即严格$<$),则称$f$是严格凸函数
$f(\lambda x_1+(1-\lambda)x_2)\leq\lambda f(x_1)+(1-\lambda)f(x_2)$

凸集与凸函数的关系
凸集和凸函数之间有密切的联系
- 凸函数的下水平集是凸集:
- 如果$f$是凸函数,那么对于任意$\alpha\in\mathbb{R}$,集合$\{x\mid f(x)\leq\alpha\}$是凸集
- 这一性质常用于证明优化问题的可行域是凸集
- 凸优化问题的可行域是凸集:
- 凸优化问题中,目标函数是凸函数,约束条件是凸集,因此可行域是凸集
凸问题
凸问题在数学和机器学习中非常重要,因为凸问题具有良好的性质:能够保证找到的局部最优解就是全局最优解。一个优化问题被称为凸问题,如果它满足以下条件:
- 目标函数是凸函数
- 最小化问题中,目标函数$f(x)$是凸函数
- 最大化问题中,目标函数$f(x)$是凹函数
- 可行域是凸集:
- 不等式约束${g}_{i}(x)\leq0$中的函数${g}_{i}(x)$是凸函数
- 等式约束$h_j(x)=0$中的函数$h_j(x)$是仿射函数(即$h_j(x)=a_j^\top x+b_j$)
凸问题的一般形式可以写成
$\begin{aligned}\text{min}\;&f(x)\\s.t.\;&g_i(x)\leq0,\quad i=1,2,\ldots,m\\&h_j(x)=0,\quad j=1,2,\ldots,p\end{aligned}$
其中$f(x)$和 $g_i(x)$ 是凸函数,$h_j(x)$是仿射函数。
凸问题具有以下重要性质
- 局部最优解就是全局最优解
- 最优解的唯一性
- 如果目标函数是严格凸函数,那么最优解是唯一的
- 高效的求解方法
- 凸问题可以通过许多高效的算法求解,例如梯度下降法、牛顿法、内点法等
- 对偶性
- 凸问题通常具有强对偶性,即原问题和对偶问题的最优值相等
对偶问题
由于拉格朗日乘数法求出的极值不一定是最值,如下面一种非凸问题的情况
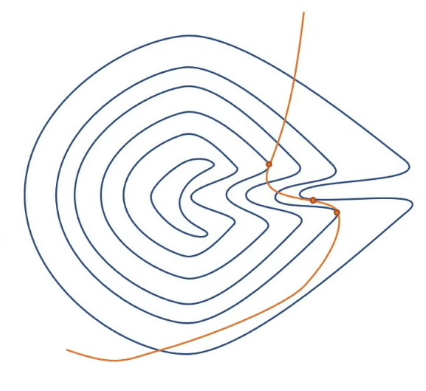
假如我们碰到了一个非凸问题,该怎么求解呢?我们可以看该非凸问题拉格朗日函数的对偶问题。假设有如下一般问题
$\begin{aligned}\text{min}\;&f_0(x),x\in\mathbb R^n\\s.t.\;&f_i(x)\leq0,\quad i=1,2,\ldots,m\\&h_i(x)=0,\quad i=1,2,\ldots,p\end{aligned}\qquad (p1)$
则通过拉格朗日乘数可以将该问题转换为如下问题形式
$L(x,\lambda,v)=f_{0}(x)+\sum\lambda_{i}f_{i}\left(x\right)+\sum\nu_{i}h_{i}\left(x\right)$
原问题:$\begin{aligned}&\min_{x}\max_{\lambda,\nu}L(x,\lambda,\nu)\\&s.t.\lambda\geq0\end{aligned}\qquad(p2)$
上述两个问题是等价的,问题$p1$的两个约束条件,实际上被转化到问题$p2$的中$\max_{\lambda,\nu}L(x,\lambda,\nu)$了。问题$p2$中$x$的可行域实际上是整个欧式空间$\mathbb R^n$。
下面针对问题$p2$中$x$的可行域进行分类讨论
$\begin{cases}x\text{不在可行域内:}&\max_{\lambda,\nu}L(x,\lambda,\nu)=f_0(x)+\infty+\infty=\infty\\x\text{在可行域内:}&\max_{\lambda,{\nu}}L({x},{\lambda},{\nu})=f_0({x})+0+0=f_0({x})\end{cases}$
优化内层最大化时,可暂时将外层最小化的$x$看作常数。当$p2$的$x$不在$p1$可行域内时,有$f_i(x)>0$,而对于$p2$有约束$\lambda\ge0$,因此$\lambda_{i}f_{i}\left(x\right)>0$,对$h_i(x)$也同理。因此$x$不在$p1$可行域内时,最大化$L$为$\infty$。
当当$p2$的$x$在$p1$可行域内时,恒有$f_i(x)\ge0,\;\lambda\le0\Longrightarrow\lambda_{i}f_{i}\left(x\right)\le0$,因此$x$在$p1$可行域内时,最大化$L$为$f_0(x)+0+0=f_0(x)$。
以上即证明了问题$p1$和问题$p2$有相同的最优解,即$p1$和$p2$等价。
上述原问题拉格朗日函数的对偶问题可以表示为如下,首先找到一个对偶函数
$对偶函数:g(\lambda,\nu)={\min}_{x}L(x,\lambda,\nu)$
$\begin{aligned}对偶问题:&\max_{\lambda,\nu}g(\lambda,\nu)=\max_{\lambda,\nu}\min_{x}L(x,\lambda,\nu)\\&s.t.\lambda\geq0\end{aligned}$
直观来看,实际就是把原问题的最小-最大问题转化为了对偶问题的最大-最小问题。
进一步来看,求对偶问题内层的一元最值$\min_x$可以转化为如下梯度约束
$\begin{aligned}对偶问题:\max_{\lambda,\nu}\;&g(\lambda,\nu)\\s.t.\;&\nabla_xL(x,\lambda,\nu)=0\\&\lambda\geq0\end{aligned}$
上述问题即为原问题的对偶问题。对偶问题有一个良好的特性,即不论原问题是什么,原问题的对偶问题是一个凸问题。下面给出证明。
假设原问题的拉格朗日函数如下
$L(x,\lambda,v)=f_{0}(x)+\sum\lambda_{i}f_{i}\left(x\right)+\sum\nu_{i}h_{i}\left(x\right)$
原问题的拉格朗日对偶函数如下
$g(\lambda,\nu)={\min}_{x}L(x,\lambda,\nu)$
可以进一步改写为,其中$x^\star$是常数
$g({\lambda},{\nu})=f_{0}(x^{\star})+\sum\lambda_{i}f_{i}(x^{\star})+\sum\nu_{i}h_{i}(x^{\star})$
这里$g({\lambda},{\nu})$确定的是一个线性超平面,其函数是一个凹凸函数(凸函数)。而对偶问题的可行域$\lambda\le0$半空间显然是一个凸集。因此该对偶问题一定是一个凸优化问题。
原问题与对偶问题的关系
弱对偶性
(弱对偶性)原问题得出的解一定大于等于对偶问题得到的解。
下面给出证明。假设原问题为
$\begin{aligned}原问题:&\min_{x}\max_{\lambda,\nu}L(x,\lambda,\nu)\\&s.t.\lambda\geq0\end{aligned}$
原问题的拉格朗日对偶问题为
$\begin{aligned}对偶问题:&\max_{\lambda,\nu}g(\lambda,\nu)=\max_{\lambda,\nu}\min_{x}L(x,\lambda,\nu)\\&s.t.\lambda\geq0\end{aligned}$
其中拉格朗日函数如下
$L(x,\lambda,v)=f_{0}(x)+\sum\lambda_{i}f_{i}\left(x\right)+\sum\nu_{i}h_{i}\left(x\right)$
首先对于任意固定的$\lambda$和$\nu$,拉格朗日函数可看作关于$x$的一元函数,其最小值满足
$\min_xL(x,\lambda,\nu)\leq L(x,\lambda,\nu)$
因为最大值不会减小函数的值,两边同时取最大值。
$\max_{\lambda,\nu}\min_xL(x,\lambda,\nu)\leq\max_{\lambda,\nu}L(x,\lambda,\nu)$
右边取最小值。此时左边已经是定值,而右边也可看作关于$x$的一元函数,因此有
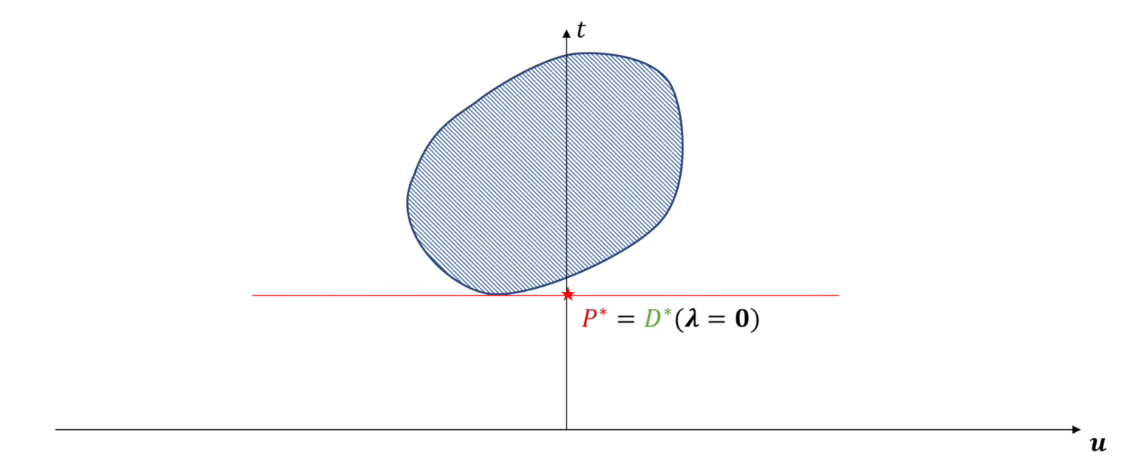
$D^*=\max_{\lambda,\nu}\min_xL(x,\lambda,\nu)\leq\min_x\max_{\lambda,\nu}L(x,\lambda,\nu)=P^*$
其中$P^*$为原问题的解,$D^*$为对偶问题的解,因此原问题得出的解一定大于等于对偶问题得到的解$P^*\ge D^*$,这一性质也叫弱对偶性。
举个例子通俗来说,即“凤尾”$\ge$“鸡头”。何谓“凤尾”?我先选出最强的一批人$\max f$,然后组成实验班,实验班倒数第一就是$\min\;\max f$;何谓“鸡头”?我先选出最弱的一批人$\min f$,然后在这批比较弱的人当中选出最强的那个人,也即是$\max\;\min f$。
下面是一个直观的几何证明
首先是原始版本的原问题
$\begin{aligned}\text{min}\;&f_0(x),x\in\mathbb R^n\\s.t.\;&f_i(x)\leq0,\quad i=1,2,\ldots,m\\&h_i(x)=0,\quad i=1,2,\ldots,p\end{aligned}\qquad (p1)$
及其拉格朗日对偶问题
$\begin{aligned}对偶问题:&\max_{\lambda,\nu}g(\lambda,\nu)=\max_{\lambda,\nu}\min_{x}L(x,\lambda,\nu)\\&s.t.\lambda\geq0\end{aligned}$
下面我们对拉格朗日函数做一些简化(注意$h_i(x)=0$,但$h_i^\prime(x)$不一定为零)
$L(x,\lambda,v)=f_{0}(x)+\sum\lambda_{i}f_{i}\left(x\right){\color{lightgray}+\sum\nu_{i}h_{i}\left(x\right)}=\mathbf t+\mathbf{\lambda^T}\cdot \mathbf u$
其中$t$代表目标函数,$u$代表不等式约束,$\lambda$代表系数。这里$t,u$实际上都是向量,但为了简化,这里我们把它们看作变量(实际是关于$x$的函数)。则简化后,原问题的可行域可以表示为如下
$\{(t,\boldsymbol{u})|t=f_{0}(\boldsymbol{x}),u_{i}=f_{i}(\boldsymbol{x}),{\color{red}\boldsymbol{x}\in D}\}=G_{1}$
$D=\{x|f_i(x)\leq0, 其中i=1,2,\ldots,m,\;\;h_i(x)=0,其中 i=1,2,\ldots,q\}$
对偶问题的可行域如下
$\{(t,\boldsymbol{u})|t=f_0(\boldsymbol{x}),u_i=f_i(\boldsymbol{x}),{\color{red}\boldsymbol{x}\in\mathbb{R}^n}\}=G_2$
因此简化后拉格朗日原问题可以表示为如下形式
$\text{原问题:}\min_x\;\{t|(t,\boldsymbol{u})\in G_1,{\color{lightgray}u\leq0}\}$
对偶问题可以简化为如下
$\text{对偶问题:}\max_{\lambda}\min_x\;\{t+\lambda^T\cdot u|(t,\boldsymbol{u})\in G_2,{\color{red}\lambda\ge0}\}$
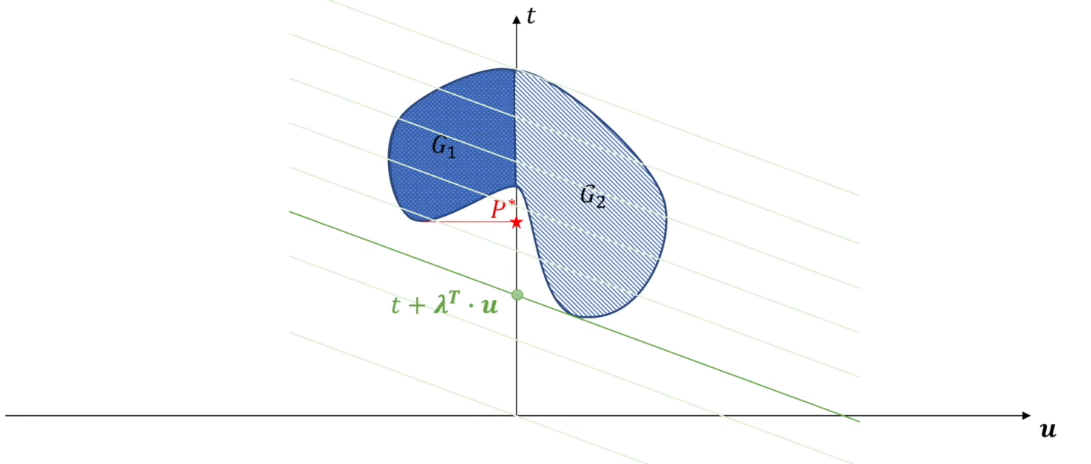
首先看下面的一般情况,其中$G_1+G_2$为对偶问题的可行域,$G_1$为原问题的可行域。显然这里的$P^*$就是原问题在可行域$G_1$下的解($\min t$)

下面来看对偶问题的解,即$\max_{\lambda}\;\min_x t+\lambda^T\cdot u$,这里可以将$t+\lambda^T\cdot u$看作一条直线。先看内层的最小化,即最小化该直线的截距
下面再看外层的最大化$\max_{\lambda}$,相当于在满足最小化的情况下只调整直线斜率
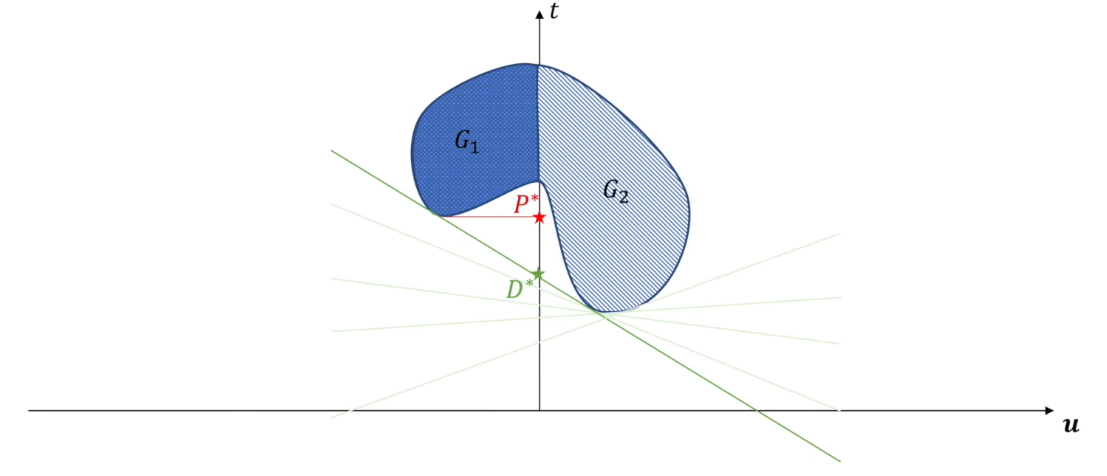
最终找到对偶问题的解为$D^*$,显然这里满足$P^*\ge D^*$。
强对偶性
如果原问题是凸问题且满足某些约束条件(如 Slater 条件),则强对偶性成立
$g(\lambda^*,\nu^*)=f(x^*)$
即对偶问题的最优值等于原问题的最优值$P^*=D^*$。下面是一个强对偶的例子

Slater 条件
当原问题为凸问题,且满足如下的Slater条件时,强对偶性成立
$\begin{aligned}\text{Slater条件:}&存在一个点x\in relint\;D\\&使得f_i(x)<0,\quad其中i=1,2,3,\ldots,m,\;\;Ax=b\\&(relint\;D表示可行域D的相对内部)\end{aligned}$
这里$f_i(x)<0$表示原问题的不等式约束条件严格满足,$Ax=b$表示原问题的等式仿射约束精确满足。其中$x$位于可行域的相对内部,即非边界部分。Slater条件实际上保证了可行域不能退化为一点。如果等式约束$h_i(x)$不是仿射函数,Slater条件可能无法直接应用。

直观来看,如果将原问题转化为上述的$(t,u)$原问题,则Slater条件实际上保证了可行域在$u<0$的部分至少存在一点。
$\text{原问题:}\min_x\;\{t|(t,\boldsymbol{u})\in G_1,{\color{lightgray}u\leq0}\}$
Slater条件只是强对偶性的一个充分条件,也就是说一个强对偶问题不一定满足Slater条件。虽然目前仍不清楚强对偶问题的充要条件,但强对偶问题的必要条件是KKT条件,即一个强对偶问题一定满足KKT条件。当找到一个问题的最优点,则该点一定满足KKT条件,反之则不成立。
KKT条件(Karush-Kuhn-Tucker Conditions)
首先给出一般原凸优化问题,其中$f_0(x),f_i(x)$是凸函数,$h_i(x)$是仿射函数。
$\begin{aligned}\text{min}\;&f_0(x),x\in\mathbb R^n\\s.t.\;&f_i(x)\leq0,\quad i=1,2,\ldots,m\\&h_i(x)=0,\quad i=1,2,\ldots,p\end{aligned}$
其对偶问题如下
$\begin{aligned}对偶问题:\max_{\lambda,\nu}\;&g(\lambda,\nu)\\s.t.\;&\nabla_xL(x,\lambda,\nu)=0\\&\lambda\geq0\end{aligned}$
如果该凸优化问题是一个强对偶问题,则一定满足KKT条件。其中KKT条件包含以下五个子条件
$\begin{aligned}&\begin{cases}f_i(x)\le0\\h_i(x)=0\end{cases}\quad(解x必须满足原始问题的约束)&原问题可行条件\\\\&\begin{cases}\nabla_xL(x,\lambda,\nu)=0\\\lambda\geq0\end{cases}\quad(解x必须满足对偶问题的约束)&对偶可行条件\\\\&\lambda_if_i(x)=0&互补松弛条件\end{aligned}$
这里的互补松弛条件,实际上就是上面提到的松弛紧致约束的另一种写法,同时包含了松弛约束和紧致约束
当一个凸优化问题满足Slater条件时,该问题是一个强对偶问题,我们可以通过KKT条件来求解该问题的最优解。
使用KKT条件求解最优值
下面是一个具体的例子,原问题表述如下,其显然是一个凸优化问题,且满足Slater条件,因此是一个强对偶问题
$\begin{aligned}\text{min}\;&f_0(x)=x_1^2+x_2^2,x\in\mathbb R^n\\s.t.\;&f_1(x)=x_1+x_2-1\leq0,\\&h_1(x)=x_1-x_2=0\end{aligned}$
其拉格朗日函数如下
$\mathcal{L}(x,\lambda,\nu)=x_1^2+x_2^2+\lambda(x_1+x_2-1)+\nu(x_1-x_2)$
应用KKT条件如下
$\begin{aligned}&\begin{cases}x_1+x_2-1\leq0\\x_1-x_2=0\end{cases}\quad&原问题可行条件\\\\&\begin{cases}\frac{\partial\mathcal{L}}{\partial x_1}=2x_1+\lambda+\nu=0\\\frac{\partial\mathcal{L}}{\partial x_2}=2x_2+\lambda-\nu=0\\\lambda\geq0\end{cases}\quad&对偶可行条件\\\\&\lambda(x_1+x_2-1)=0&互补松弛条件\end{aligned}$
最终可以解得最优解为$f_0(0,0)=0$
多重梯度下降对偶问题
承接上文,我们已经将多重梯度下降问题改写为如下形式的约束问题
$\begin{cases}(d_k,\alpha_k)=\min\{\alpha+\frac{1}{2}||d||^2\}\\ s.t.\quad\nabla f_i(x_k)^Td\leq\alpha&\end{cases}$
其中$\alpha=\max_i\nabla f_i(x_k)^Td$。然而该问题不好直接求解,我们可以找到其拉格朗日对偶问题
首先引入该问题的拉格朗日函数
$L(d,\alpha,\lambda)=\alpha+\frac{1}{2}||d||^2+\sum_{i=1}^m\lambda_i(\nabla f_i(x_k)^Td-\alpha)$
对偶函数如下,即拉格朗日函数关于$d$和$\alpha$的下确界(最小化)
$g(\lambda)=\inf_{d,\alpha}L(d,\alpha,\lambda)$
使用KKT条件求解该最小优化问题,直接分别求偏导即可
$\frac{\partial L}{\partial\alpha}=1-\sum_{i=1}^m\lambda_i=0\Longrightarrow\sum_{i=1}^m\lambda_i=1$
$\frac{\partial L}{\partial d}=d+\sum_{i=1}^m\lambda_i\nabla f_i(x_k)=0\Longrightarrow d=-\sum_{i=1}^m\lambda_i\nabla f_i(x_k)$
然后将$d$和$\alpha$的表达式代入拉格朗日函数
$\begin{aligned}g(\lambda)=\inf_{d,\alpha}L(d,\alpha,\lambda)&=\alpha+\frac{1}{2}||d||^2+\sum_{i=1}^m\lambda_i(\nabla f_i(x_k)^Td-\alpha)\\&=\frac{1}{2}||d||^2+\sum_{i=1}^m\lambda_i\nabla f_i(x_k)^Td\\&=\frac{1}{2}\left\|-\sum_{i=1}^m\lambda_i\nabla f_i(x_k)\right\|^2+\sum_{i=1}^m\lambda_i\nabla f_i(x_k)^T\left(-\sum_{j=1}^m\lambda_j\nabla f_j(x_k)\right)\\&=\frac{1}{2}\left\|\sum_{i=1}^m\lambda_i\nabla f_i(x_k)\right\|^2-\left\|\sum_{i=1}^m\lambda_i\nabla f_i(x_k)\right\|^2\\&=-\frac{1}{2}\left\|\sum_{i=1}^m\lambda_i\nabla f_i(x_k)\right\|^2\end{aligned}$
对偶问题可以表示为最大化对偶函数
$\max_\lambda g(\lambda)=\max_\lambda\left(-\frac{1}{2}\left\|\sum_{i=1}^m\lambda_i\nabla f_i(x_k)\right\|^2\right)$
等价于最小化$\left\|\sum_{i=1}^m\lambda_i\nabla f_i(x_k)\right\|^2$,因此多重梯度下降问题的对偶问题可以表示成如下
$\begin{aligned}\arg \min_\lambda\;&\left\|\sum_{i=1}^m\lambda_i\nabla f_i(x_k)\right\|^2\\ s.t.&\;\sum_{i=1}^m\lambda_i=1,\quad\lambda_i\geq0\end{aligned}$
直观来看,就是寻找一组权重向量$\lambda$,使多目标函数梯度加权和的$L2$范数平方最小
多任务学习
多任务学习(Multi-Task Learning, MTL)是一种机器学习范式,旨在通过同时学习多个相关任务来提高模型的泛化能力和性能。与单任务学习不同,MTL通过共享任务之间的信息,利用任务之间的相关性来增强模型的学习效果。在多任务学习中,部分模型参数是多个任务共享的。这些共享参数捕捉任务之间的共同特征和结构。除了共享参数外,每个任务还有自己特定的参数,用于捕捉任务独有的特征。
Ozan Sener等人的研究表明,多任务学习本质是一个多目标优化问题。多任务学习的形式化定义如下
考虑一个多任务学习问题,输入空间为$\mathcal X$,任务集空间为${\mathcal{Y}^{t}}_{t\in[T]}$,给定一个包含$N$个个独立同分布数据点的数据集$\{x_{i},y_{i}^{1},\ldots,y_{i}^{T}\}_{i\in[N]}$,其中$N$表示任务个数,$y_i^t$是第$t$个任务的第$i$个数据点的标签。则第$t$个任务特征提取过程可以表示为
$f^t(\mathbf{x};\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t):\mathcal{X}\to\mathcal{Y}^t$
其中$\boldsymbol{\theta}^{sh}$是任务共享参数,$\boldsymbol{\theta}^t$是第$t$个任务特有参数。每个任务的损失函数如下
$\mathcal{L}^{t}(\cdot,\cdot):\mathcal{Y}^{t}\times\mathcal{Y}^{t}\to\mathbb{R}^{+}$
多任务学习的目标是以下的经验风险最小化公式
$\begin{aligned}\min_{\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^1,\ldots,\boldsymbol{\theta}^T}\sum_{t=1}^Tc^t\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)\end{aligned}$
其中$c^t$是每个任务的权重,$\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)$是第$t$个任务的经验损失,定义如下
$\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)\triangleq\frac{1}{N}\sum_i\mathcal{L}(f^t(x_i;\theta^{sh},\theta^t),y_i^t)$
这里第$t$个任务的经验损失代表了模型在所有数据点上的预测与真实标签之间的损失均值。
尽管加权求和公式十分直观,但它通常需要进行昂贵的网格搜索(grid search)来调整不同任务的权重,或者使用启发式方法搜索权重向量。加权求和的另外一个问题是难以定义全局最优性。如考虑两组解$\theta,\overline\theta$,对某些任务$t_1,t_2$同时有
$\hat{\mathcal{L}}^{t_{1}}(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^{t_{1}})<\hat{\mathcal{L}}^{t_{1}}(\bar{\boldsymbol{\theta}}^{sh},\bar{\boldsymbol{\theta}}^{t_{1}})$
$\hat{\mathcal{L}}^{t_{2}}(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^{t_{2}})>\hat{\mathcal{L}}^{t_{2}}(\bar{\boldsymbol{\theta}}^{sh},\bar{\boldsymbol{\theta}}^{t_{2}})$
此时$\theta$在任务$t_1$中表现更好,$\bar\theta$在任务$t_2$中表现更好。在不知道任务之间相对重要性的情况下,无法比较这两组解哪个更好。
因此作者将一个多任务学习MTL问题看作一个多目标优化问题:优化一组可能相互冲突的目标函数。首先使用向量值损失函数$\mathbf L$形式化定义MTL的多目标优化形式
$\begin{aligned}\min_{\theta^{sh},\theta^1,\ldots,\theta^T}\mathbf L(\theta^{sh},\theta^1,\ldots,\theta^T)=\min_{\theta^{sh},\theta^1,\ldots,\theta^T}\left(\hat{\mathcal{L}}^1(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^1),\ldots,\hat{\mathcal{L}}^T(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^T)\right)^{\mathrm T}\end{aligned}$
多目标优化的目标是达到帕累托最优(Pareto optimality)。
MTL下的帕累托最优(Pareto optimality)
$\textbf{(定义1. \;\;帕累托支配\;Pareto-domination)}$ 对于任意的两个解$\theta,\bar\theta\in\Omega$,解$\theta$支配解$\bar\theta$时,记作$\theta\prec\bar{\theta}$,则对于所有的任务$t$有
$L^i(\theta^\mathrm{sh},\theta^i)\leqslant L^i(\bar{\theta}^\mathrm{sh},\bar{\theta}^i),\forall i\in(1,2,\cdots,T),$
且$L^{j}(\theta^{\mathrm{sh}},\theta^{j})<L^{j}(\bar{\theta}^{\mathrm{sh}},\bar{\theta}^{j}),\exists j\in(1,2,\cdots,T)$
$\textbf{(定义2. \;\;帕累托最优解\;Pareto-optimality)}$ 如果不存在解$\theta(\theta\in\Omega)$使得$\theta\prec{\theta}^*$,则称解$\theta^*$为Pareto最优解。所有Pareto最优解构成的集合称为Pareto集$\mathcal{P}_{\theta}$, Pareto集中所有Pareto最优解在目标空间的映射形成的解集组成Pareto最优解的目标向量值集合, 该集合称为Pareto前沿$\mathcal{P}_{\mathbf{L}}={\mathbf{L}(\boldsymbol{\theta})}_{\boldsymbol{\theta}\in\mathcal{P}_{\boldsymbol{\theta}}}$。帕累托前沿表示在多目标优化中所有可能的帕累托最优解在损失空间中的分布。
$\textbf{(定义3. \;\;帕累托稳定点\;Pareto-stationarity)}$假设$\theta^0\in\Omega$是多目标优化问题中的一个可行解。$u_i=\nabla L^i(\theta^0)$是目标函数$L^i$在点$\theta^0$处的梯度向量。如果存在一组约束权重$\lambda_i$使得这些梯度的凸组合为零
$\begin{aligned}&\sum_{i=1}^n\lambda_iu_i=0\\&s.t.\;\sum_{i=1}^n\lambda_i=1,\;\;\lambda_i\ge0\end{aligned}$
则称$\theta^0$为帕累托稳定点
多重梯度下降算法(Multiple Gradient Descent Algorithm, MGDA)
与单目标优化类似,多目标优化也可以通过梯度下降来求解局部最优解。上文已经分析过,可以使用KKT条件来求解该问题。在多任务学习MTL场景下,对于任务特定参数和共享参数,KKT条件如下(可分别看作多任务最优和单任务最优)
$\begin{aligned}&存在\alpha^{1},\ldots,\alpha^{T}\geq0,使得\sum_{t=1}^{T}\alpha^{t}=1且\sum_{t=1}^{T}\alpha^{t}\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^{t}(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^{t})=0\\&对所有任务t有\nabla_{\boldsymbol{\theta}^t}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)=0\end{aligned}$
任何满足这些条件的解被称为帕累托稳定点(Pareto stationary point)。每个帕累托最优点都是帕累托稳定点,但反之则不一定成立。
考虑以下优化问题,实际上就是多目标优化的对偶问题,上文已经推导过
$\begin{aligned}\min_{\alpha^{1},…,\alpha^{T}}\left\{\left\|\sum_{t=1}^{T}\alpha^{t}\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^{t}(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^{t})\right\|_{2}^{2}\;\;\middle|\;\;\sum_{t=1}^{T}\alpha^{t}=1,\alpha^{t}\geq0\quad\forall t\right\}\end{aligned}\qquad(p1)$
Désidéri等证明了上述优化问题的解以下有两种情况
- 这个优化问题的解为是0,此时得到的解满足KKT条件
- 得到的解提供了所有任务的下降方向
MGDA的求解
求解问题$p1$等价于在输入点的凸包中找到最小范数点。在计算几何中,该问题等价于在凸包中找到与给定查询点最近的点。然而以往计算几何领域的研究并不适用于MTL场景。在计算几何文献中,算法通常处理的是在低维空间(通常是2维或3维)中大量点的凸包中找到最小范数点的问题。在MTL场景下,点的数量是任务的数量通常较少,而维度是共享参数的数量可能达到数百万。因此作者采用了一种基于凸优化的方法。
两任务的情况
在考虑一般情况之前,首先考虑两任务优化的情况
$\begin{aligned}\min_{\alpha\in[0,1]}\left\|\alpha\nabla_{\theta^{sh}}\hat{\mathcal{L}}^1(\theta^{sh},\theta^1)+(1-\alpha)\nabla_{\theta^{sh}}\hat{\mathcal{L}}^2(\theta^{sh},\theta^2)\right\|_2^2\end{aligned}$
简化为
$\begin{aligned}\min_{\alpha\in[0,1]}\left\|\alpha\theta+(1-\alpha)\bar{\theta}\right\|_2^2\end{aligned}\qquad(p2)$
其中$\theta$表示$\nabla_{\theta^{sh}}\hat{\mathcal{L}}^1(\theta^{sh},\theta^1)$,$\bar{\theta}$表示$\nabla_{\theta^{sh}}\hat{\mathcal{L}}^2(\theta^{sh},\theta^2)$。
对问题$p2$进行求导取求最值。首先展开$p2$
$\begin{aligned}\left\|\alpha\theta+(1-\alpha)\bar{\theta}\right\|_2^2&=(\alpha\theta+(1-\alpha)\bar{\theta})^\top(\alpha\theta+(1-\alpha)\bar{\theta})\\&=\alpha^2\theta^\top\theta+(1-\alpha)^2\bar{\theta}^\top\bar{\theta}+2\alpha(1-\alpha)\theta^\top\bar{\theta}\\&=\alpha^2\left\|\theta\right\|_2^2+(1-\alpha)^2\left\|\bar{\theta}\right\|_2^2+2\alpha(1-\alpha)\theta^\top\bar{\theta}=f(\alpha)\end{aligned}$
对$f(\alpha)$进行求导并令其等于零
$\frac{df(\alpha)}{d\alpha}=2\alpha\left\|\theta\right\|_2^2-2(1-\alpha)\left\|\bar{\theta}\right\|_2^2+2(1-2\alpha)\theta^\top\bar{\theta}=0$
得到
$\alpha\left\|\theta\right\|_2^2-(1-\alpha)\left\|\bar{\theta}\right\|_2^2+(1-2\alpha)\theta^\top\bar{\theta}=0$
$\alpha(\left\|\theta\right\|_2^2+\left\|\bar{\theta}\right\|_2^2-2\theta^\top\bar{\theta})=\left\|\bar{\theta}\right\|_2^2-\theta^\top\bar{\theta}$
最终解得$\alpha$
$\begin{aligned}\alpha&=\frac{\left\|\bar{\theta}\right\|_2^2-\theta^\top\bar{\theta}}{\left\|\theta\right\|_2^2+\left\|\bar{\theta}\right\|_2^2-2\theta^\top\bar{\theta}}\\&=\frac{\left\|\bar{\theta}\right\|_2^2-\theta^\top\bar{\theta}}{\left\|\theta-\bar{\theta}\right\|_2^2}\\&=\frac{\left(\bar\theta-\theta\right)^\top\bar\theta}{\left\|\theta-\bar{\theta}\right\|_2^2}\end{aligned}$
由于约束条件,$\alpha\in[0,1]$,因此需要对解进行裁剪
- 如果$\alpha<0$,则取$\alpha=0$
- 如果$\alpha>1$,则取$\alpha=1$
因此最终两任务优化解析解为
$\begin{aligned}&\alpha=\begin{cases}0,&\mathrm{if~}\theta^\top\bar{\theta}\geq\left\|\theta\right\|_2^2,\\\frac{||\bar{\theta}||_2^2-\theta^\top\bar{\theta}}{||\theta-\bar{\theta}||_2^2},&\mathrm{if~}\theta^\top\bar{\theta}<||\theta||_2^2\;\mathrm{and~}\;\theta^\top\bar{\theta}<||\bar{\theta}||_2^2,\\1,&\mathrm{if~}\theta^\top\bar{\theta}\geq\left\|\bar{\theta}\right\|_2^2.&\end{cases}\end{aligned}$
上述解析解的几何意义如下
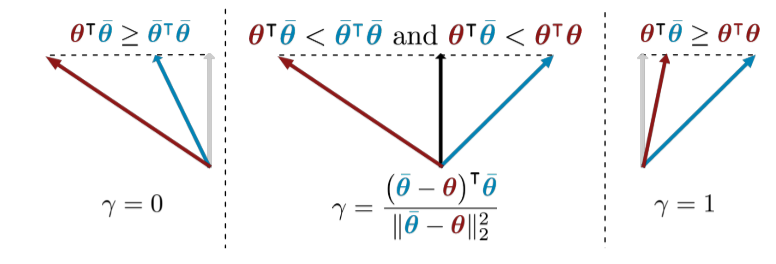
- 当$\theta^\top\bar{\theta}\geq||\theta||_2^2$时,任务1的梯度$\theta$与任务2的梯度$\bar\theta$的方向非常接近,此时$\alpha=0$,即完全依赖任务2
- 当$\theta^\top\bar{\theta}<||\theta||_2^2\;\mathrm{and~}\;\theta^\top\bar{\theta}<||\bar{\theta}||_2^2$时,任务1和任务2的梯度方向不一致,此时$\alpha$取中间值平衡两个任务的梯度
- 当$\theta^\top\bar{\theta}\leq||\theta||_2^2$时,任务2的梯度$\bar\theta$与任务1的梯度$\theta$的方向非常接近,此时$\alpha=1$,即完全依赖任务1
多任务的情况
上述是任务数$n=2$的情况,当任务数$n>2$时可以通过Frank-Wolfe算法将问题转化为多个$n=2$的情况进行迭代。
其中MTL的参数更新流程如下
- $\textbf{for}\;t=1\;\textbf{to}\;T\;\textbf{do}$
- $\quad\theta^t=\theta^t-\eta\nabla_{\theta_t}\hat{\mathcal {L}}^t(\theta^{sh},\theta^t)$
- $\textbf{end for}$
- $\alpha^1,\ldots,\alpha^T=\textbf{Frank-Wolfe-Solver}(\theta)$
- $\theta^{sh}=\theta^{sh}-\eta\sum^T_{t=1}\alpha^t\nabla_{\theta^{sh}}\hat{\mathcal {L}}^t(\theta^{sh},\theta^t)$
首先使用梯度下降循环更新任务特定参数$\theta^t$,然后通过Frank-Wolfe算法求解权重寻找一个共同的下降方向,最后通过梯度下降沿着一个共同的下降方向更新共享权重。
Frank-Wolfe算法
Frank-Wolfe算法(也称为条件梯度法,Conditional Gradient Method)是一种用于求解带约束的凸优化问题的迭代算法。Frank-Wolfe算法的核心思想是通过在每次迭代中线性化目标函数,并在约束集上求解线性规划问题来找到一个可行的下降方向,然后沿着这个方向进行一维搜索来更新解。
Frank-Wolfe算法的主要步骤如下
- 线性化目标函数:
- 在当前点$x_k$处,对目标函数$f(x)$进行线性近似:
$f(x)\approx f(x_k)+\nabla f(x_k)^\top(x-x_k)=f(x_k)-\nabla f(x_k)^\top x_k+\nabla f(x_k)^\top x$ - 线性化后的目标函数是$x$的线性函数
- 在当前点$x_k$处,对目标函数$f(x)$进行线性近似:
- 求解线性规划问题:
- 在约束集$D$上,求解线性化后的目标函数的最小值
$\begin{aligned}s_k=&\arg\min_{s}\nabla f(x_k)^\top s\\&s.t.\;s\in D\end{aligned}$ - 这个步骤通常比直接求解原问题简单,因为线性规划问题有高效的求解方法
- 在约束集$D$上,求解线性化后的目标函数的最小值
- 确定下降方向:
- 下降方向为$d_k=s_k-x_k$,即从当前点$x_k$指向线性规划问题的最优解$s_k$
- 一维搜索:
- 沿着下降方向$d_k$进行一维搜索,找到最优步长$\gamma_k$
$\begin{aligned}\gamma_k=&\arg\min_{\gamma}f(x_k+\gamma d_k)\\&s.t.\;\gamma\in [0,1]\end{aligned}$ - 更新当前点$x_{k+1}=x_k+\gamma_kd_k$
- 沿着下降方向$d_k$进行一维搜索,找到最优步长$\gamma_k$
- 迭代:
- 重复上述步骤,直到满足收敛条件(如梯度足够小或迭代次数达到上限)
Frank-Wolfe算法只需要求解线性规划问题,而不需要投影操作(Projection)。当约束集$D$是简单的凸集(如单纯形、球等)时,线性规划问题可以高效求解,因此Frank-Wolfe算法适用于大规模优化问题。
但Frank-Wolfe算法的收敛速度通常是次线性的(sublinear),尤其是在接近最优解时,收敛速度会变慢。算法的性能可能对初始点$x_0$的选择敏感,尤其是在非强凸目标函数的情况下。
Frank-Wolfe算法在MGDA中的应用
在MGDA中,Frank-Wolfe算法用于求解多任务学习中的共享参数优化问题,目标是找到一个能够平衡多个任务损失的下降方向,也即找到一组$\alpha=(\alpha^1,\alpha^2,\ldots,\alpha^T)$,使得
$\text{最优更新方向}=\sum_{t=1}^T\alpha^t\nabla_{\theta^{sh}}L^t(\theta^{sh},\theta^t)$
$\textbf{Frank-Wolfe-Solver}$具体流程如下
- 计算各任务损失和共享参数梯度:
- 计算各任务的损失函数$\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)$,及各任务在共享参数上的梯度$\nabla_{\theta^{sh}}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)$
- $\nabla_{\theta^{sh}}\hat{\mathcal{L}}^t(\theta^{sh},\theta^t)$指示了各任务在共享参数上的下降情况,从而确定下一步如何更新参数$\theta^{sh}$
- 初始化任务权重:
- 均匀初始化所有任务的权重为$\alpha=(\alpha^{1},\ldots,\alpha^{T})=(\frac{1}{T},\ldots,\frac{1}{T})$
- 初始时,所有任务的权重相同,表示没有先验知识表明某个任务更重要。随着算法的迭代,权重会根据任务的梯度信息进行调整。
- 计算梯度矩阵:
- 计算所有损失函数关于共享参数的梯度矩阵$M$,其中$M_{i,j\in[0,T]}=(\nabla_{\theta^{sh}}\hat{\mathcal{L}}^i(\theta^{sh},\theta^i))^T(\nabla_{\theta^{sh}}\hat{\mathcal{L}}^j(\theta^{sh},\theta^j))$
- 其中每个元素$M_{i,j}$是任务$i$和任务$j$的共享参数梯度的内积,在一些论文中也称其为“任务亲和度”
- 任务亲和度衡量了两个任务之间是否冲突,当任务亲和度为负时说明梯度方向夹角为钝角,两个任务是冲突的,反之则不冲突
- 梯度矩阵$M$衡量了所有任务两两之间的任务亲和度。通过分析$M$,可以找到能够平衡多个任务损失的下降方向
- 计算最优索引:
- 计算共享参数梯度矩阵$M$所对应的最优索引$\hat{t}=\arg\min_{\gamma}\sum_{t}\alpha^{t}M_{\gamma t}$
- 这一步的目的是找到一个最优任务索引$\hat t$,其梯度方向能够最大程度地减少所有任务的加权损失
- 线性搜索:
- 基于两任务情况的解析解进行线性搜索$\hat{\gamma}=\arg\min_\gamma((1-\gamma)\alpha+\gamma M_{\hat t})^TM((1-\gamma)\alpha+\gamma M_{\hat t})$
- 线搜索是为了确定在当前方向$M_{\hat t}$上,参数更新的最佳步长$\hat\gamma$,以确保目标函数能够快速收敛
- 更新权重$\alpha$:
- 基于最优步长$\hat\gamma$更新权重$\alpha=(1-\hat{\gamma})\alpha+\hat{\gamma}M_{t}$
- 更新权重可以逐步调整每个任务对共享参数的影响,使得优化过程能够更好地平衡多个任务
- 判断收敛:
- 循环步骤$\textbf{4-6}$,当达到迭代次数上限,或者更新步长趋于零时$\hat\gamma\sim 0$停止迭代
- 返回任务权重$\alpha^1,\ldots,\alpha^T$
这里对$\textbf{步骤5}$线性搜索的计算公式做一下推导。首先MGDA可以看作以下优化问题
$\begin{aligned}\min_{\alpha^{1},…,\alpha^{T}}\left\{\left\|\sum_{t=1}^{T}\alpha^{t}\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^{t}(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^{t})\right\|_{2}^{2}\;\;\middle|\;\;\sum_{t=1}^{T}\alpha^{t}=1,\alpha^{t}\geq0\quad\forall t\right\}\end{aligned}\qquad(p1)$
其目标函数可以表示为如下形式
$\begin{aligned}f(\alpha)=\left\|\sum_{t=1}^{T}\alpha^{t}\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^{t}(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^{t})\right\|_{2}^{2}\end{aligned}$
进一步改写
$\begin{aligned}f(\alpha)&=\left\|\sum_{t=1}^{T}\alpha^{t}\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^{t}(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^{t})\right\|_{2}^{2}\\&=\left(\sum_{t=1}^T\alpha^t\nabla_{\theta^{sh}}\hat{\mathcal L}^t(\theta^{sh},\theta^t)\right)^\top\left(\sum_{t=1}^T\alpha^t\nabla_{\theta^{sh}}\hat{\mathcal L}^t(\theta^{sh},\theta^t)\right)\\&=\left(\nabla_{\theta^{sh}}\hat{\mathcal L}^i(\theta^{sh},\theta^t)\alpha\right)^\top\left(\nabla_{\theta^{sh}}\hat{\mathcal L}^j(\theta^{sh},\theta^t)\alpha\right)\\&=\alpha^\top\left(\nabla_{\theta^{sh}}\hat{\mathcal L}^i(\theta^{sh},\theta^t)\right)^\top\left(\nabla_{\theta^{sh}}\hat{\mathcal L}^j(\theta^{sh},\theta^t)\right)\alpha\\&=\alpha^\top M\alpha\end{aligned}$
因此MGDA实际上是一个带有线性约束的凸二次型问题。其中两任务优化问题是上面问题解的特例。
MGDA最终算法流程
通过上面的分析,我们能够得到MGDA算法的完整流程
- 算法名称:$\textbf{MGDA(MOO-MTL)}$
- 算法输入:学习率$\eta$,迭代终止条件$\textbf S$,任务集合$\{T_t\}$
- 算法输出:任务共享参数$\theta^{sh}$,任务特定参数$\theta^t$
- 算法流程:
- $\textbf{for}\;t=1\;\textbf{to}\;T\;\textbf{do}$
- $\quad\theta^t=\theta^t-\eta\nabla_{\theta_t}\hat{\mathcal {L}}^t(\theta^{sh},\theta^t)\qquad(循环更新任务特定参数)$
- $\textbf{end for}$
- $\textbf {procedure}\quad\textbf{Frank-Wolfe-Solver}(\theta)$
- $\quad$均匀初始化任务权重$\alpha=(\alpha^{1},\ldots,\alpha^{T})=(\frac{1}{T},\ldots,\frac{1}{T})$
- $\quad$计算梯度矩阵$M$,其中$M_{i,j\in[0,T]}=(\nabla_{\theta^{sh}}\hat{\mathcal{L}}^i(\theta^{sh},\theta^i))^T(\nabla_{\theta^{sh}}\hat{\mathcal{L}}^j(\theta^{sh},\theta^j))$
- $\quad\textbf{repeat}$
- $\qquad$计算共享参数梯度矩阵$M$所对应的最优索引$\hat{t}=\arg\min_{\gamma}\sum_{t}\alpha^{t}M_{\gamma t}$
- $\qquad$线性搜索$\hat{\gamma}=\arg\min_\gamma((1-\gamma)\alpha+\gamma M_{\hat t})^TM((1-\gamma)\alpha+\gamma M_{\hat t})$
- $\qquad$更新权重$\alpha=(1-\hat{\gamma})\alpha+\hat{\gamma}M_{t}$
- $\quad\textbf{until}\;\textbf{S}$
- $\quad\textbf {return}\;\alpha^{1},\ldots,\alpha^{T}$
- $\textbf {end procedure}$
- $\alpha^1,\cdots,\alpha^T=\textbf{Frank-Wolfe-Solver}(\theta)$
- ${\theta}^{sh}={\theta}^{sh}-\eta\sum_{t=1}^T\alpha^t\nabla_{{\theta}^{sh}}\hat{\mathcal{L}}^t({\theta}^{sh},{\theta}^t)\qquad(更新共享权重)$
- $\textbf{return}\;\theta^t,\theta^{sh}$
针对Encoder-Decoder结构的MGDA优化
上文提到的MGDA算法适用于任何基于梯度下降的优化问题。有实验表明,Frank-Wolfe算法高效且准确,通常能够在较少的迭代次数内收敛,并且对训练时间的影响可以忽略不计。然而在MTL场景下,算法需要为每个任务$t$计算共享参数的梯度$\nabla_{{\theta}^{sh}}\hat{\mathcal{L}}^t({\theta}^{sh},{\theta}^t)$,此时需要对每个任务进行一次反向传播。由于反向传播的计算通常比前向传播更昂贵,这导致训练时间随任务数量$T$线性增长,因此对于任务数量较多的问题来说开销过大。
针对上述问题,Ozan Sener等对MGDA做了进一步优化,提出了MGDA-UB算法(MGDA-Upper Bound)。该算法通过优化目标函数的上界,只需要一次反向传播便能高效地更新共享参数$\theta^{sh}$。并且作者进一步证明,在合理的假设下,优化该上界可以得到Pareto最优解。
编码器-解码器架构
编码器-解码器架构结合了共享的表示函数和任务特定的决策函数。这类架构涵盖了大多数现有的多任务学习模型。其形式化定义如下
$f^t(\mathbf{x};\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)=(f^t(\cdot;\boldsymbol{\theta}^t)\circ g(\cdot;\boldsymbol{\theta}^{sh}))(\mathbf{x})=f^t(g(\mathbf{x};\boldsymbol{\theta}^{sh});\boldsymbol{\theta}^t)$
其中$g$代表任务共享的表示函数,$f^t$是任务特定的函数,它们以共享表示作为输入。下面进一步将共享表示写为如下形式
$\begin{aligned}&\mathbf{Z}=(\mathbf{z}_1,\ldots,\mathbf{z}_N)\\&s.t.\;\mathbf{z}_i=g(\mathbf{x}_i;\boldsymbol{\theta}^{sh})\end{aligned}$
上界推导
根据链式法则,我们可以得到原优化问题的上界
$\begin{aligned}\left\|\sum_{t=1}^T\alpha^t\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)\right\|_2^2\leq\left\|\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}\right\|_2^2\left\|\sum_{t=1}^T\alpha^t\nabla_\mathbf{Z}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)\right\|_2^2\end{aligned}$
其中$\left\|\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}\right\|_2$表示$\boldsymbol Z$对共享参数$\boldsymbol\theta^{sh}$的雅可比矩阵的范数。$\nabla_\mathbf{Z}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)$是任务$t$损失函数对表示$\boldsymbol Z$的梯度。该不等式的推导过程如下
$\begin{aligned}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)=\hat{\mathcal{L}}^t(g(\mathbf{x};\boldsymbol{\theta}^{sh}),\boldsymbol{\theta}^t)\end{aligned}$
按照链式法则对共享参数$\boldsymbol{\theta}^{sh}$求导可得
$\begin{aligned}\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)=\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}\nabla_\mathbf{Z}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)\end{aligned}$
其中$\boldsymbol Z$是共享表示$\mathbf{Z}=g(\mathbf{x};\boldsymbol{\theta}^{sh})$,$\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}$表示$\boldsymbol Z$对共享参数$\boldsymbol\theta^{sh}$的雅可比矩阵,由所有任务共享。将多个任务的梯度加权求和如下
$\begin{aligned}\sum_{t=1}^T\alpha^t\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)&=\sum_{t=1}^T\alpha^t\left(\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}\nabla_\mathbf{Z}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)\right)\\&=\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}\left(\sum_{t=1}^T\alpha^t\nabla_\mathbf{Z}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)\right)\end{aligned}$
根据矩阵范数性质$\|Av\|_2\leq\|A\|_2\cdot\|v\|_2$,平方后最终可得如下不等式
$\begin{aligned}\left\|\sum_{t=1}^T\alpha^t\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)\right\|_2^2\leq\left\|\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}\right\|_2^2\left\|\sum_{t=1}^T\alpha^t\nabla_\mathbf{Z}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)\right\|_2^2\end{aligned}$
因此我们可以通过优化不等式右侧的上界来优化左式。此外,由于$\nabla_\mathbf{Z}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)$可以在单次反向传播中计算得出,并且右式的$\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}$与$\alpha$无关,因此可以通过其上界来替代原问题的优化目标
$\begin{aligned}\min_{\alpha^1,\ldots,\alpha^T}\left\{\left\|\sum_{t=1}^{T}\alpha^{t}\nabla_{\mathbf{Z}}\hat{\mathcal{L}}^{t}(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^{t})\right\|_{2}^{2}\middle|\sum_{t=1}^{T}\alpha^{t}=1,\alpha^{t}\geq0\quad\forall t\right\}\end{aligned}\qquad\qquad(\textbf{MGDA-UB})$
MGDA-UB与Pareto最优解
MGDA-UB实际上只是原MGDA问题的一个近似,但在合理的假设下,MGDA-UB 能够产生 Pareto 最优解。假设如下
$\textbf{(定理\;1)}$假设$\frac{\partial\mathbf{Z}}{\partial\boldsymbol{\theta}^{sh}}$满秩的,并且$\alpha^1,\ldots,\alpha^T$是 MGDA-UB 的解,则以下两种情况之一成立
- $\sum_{t=1}^T\alpha^t\nabla_{\boldsymbol{\theta}^{sh}}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)=0$,并且当前点处于Pareto稳定点
- $\sum_{t=1}^T\alpha^t\nabla_{\theta^{sh}}\hat{\mathcal{L}}^t(\boldsymbol{\theta}^{sh},\boldsymbol{\theta}^t)$是一个下降方向,能够同时优化所有目标函数
使用共享表示层来代替共享参数后,模型计算复杂度将大大降低。MGDA-UB能够以较低找到一个Pareto稳定点,并且该算法可以应用于任何具有编码器-解码器模型的深度多目标优化问题。
偏好MGDA
尽管上述提出的算法能够将MTL问题转化成多目标优化问题并应用MGDA算法求得Pareto最优解,多次运行该算法能够得到Pareto前沿上的一些解。但这种算法并没有考虑不同任务之间的偏好权衡(Preference trade-off)问题。针对这一问题,Lin等提出了一种Pareto MTL算法,该算法能够得到Pareto前沿上一组具有不同权衡的解,这些解代表了不同任务之间的权衡关系。
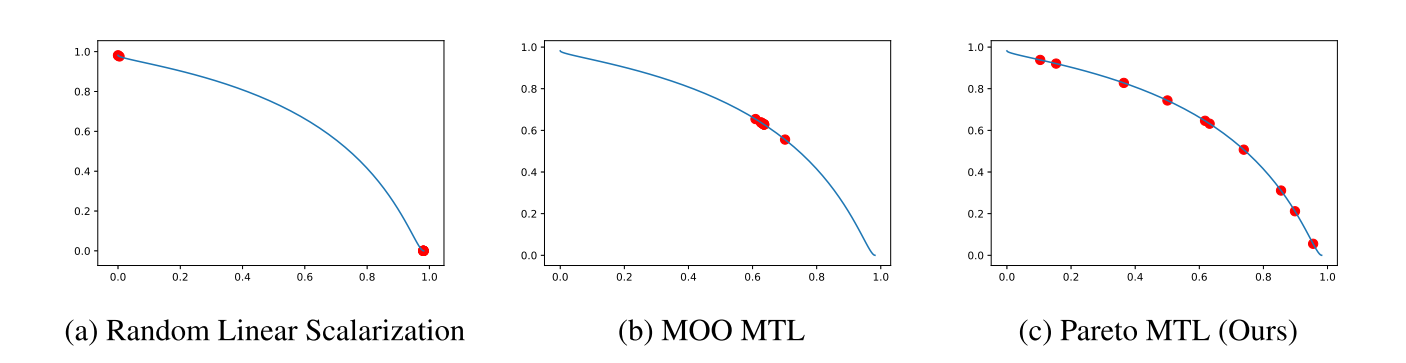
MTL子问题分解
Pareto MTL算法借鉴了基于分解的多目标进化算法,并将其推广到大规模、基于梯度的多任务学习问题中。基于分解的多目标进化算法(Decomposition-based Multi-Objective Evolutionary Algorithm)是一种流行的无梯度多目标优化方法。这类算法通过将多目标优化问题(MOP)分解为多个子问题并同时求解这些子问题来找到一组帕累托最优解。
Pareto MTL算法的主要思想是将一个多任务学习问题分解为多个约束多目标子问题,每个子问题对应一个不同的权衡偏好。通过并行求解这些子问题可以获得一组具有不同权衡的Pareto最优解。
Pareto MTL算法首先将MTL分解为$K$个子问题,其中每个子问题对应一个单位偏好向量$u_k\in\{u_1,u_2,\ldots,u_K\}\in \mathbb R^m_+$,这些偏好向量在目标空间中是均匀分布的,并且假设所有目标函数都是非负的。偏好向量将目标空间划分为不同的子区域,每个子问题对应的解被约束在对应的子区域内代表不同任务之间的权衡。每个MTL子问题的目标是在其对应的偏好子区域内找到一个Pareto解。
则偏好向量$u_k$对应的子问题的形式如下
$\begin{aligned}&\min_\theta\mathcal{L}(\theta)=(\mathcal{L}_1(\theta),\mathcal{L}_2(\theta),\cdots,\mathcal{L}_m(\theta))^T,\\& s.t.\quad\mathcal{L}(\theta)\in\Omega_k\end{aligned}\qquad (p3)$
其中$\Omega_k(k=1,\ldots,K)$是目标空间中的一个子区域,定义为
$\Omega_k=\{\boldsymbol{v}\in \mathbb R_+^m|\boldsymbol{u}_j^T\boldsymbol{v}\leq\boldsymbol{u}_k^T\boldsymbol{v},\forall j=1,\ldots,K\}$
其中$\boldsymbol{u_k}$代表子问题$k$的偏好向量,$\boldsymbol{u_j}$代表其他任意偏好向量,$\boldsymbol{v}$是子区域$\Omega_k$中的任意向量,其集合组成了$\Omega_k$。
$\boldsymbol{u}_j^T\boldsymbol{v}$代表了偏好向量$\boldsymbol{u_j}$与向量$\boldsymbol{v}$的内积,$\boldsymbol{u}_j^T\boldsymbol{v}\leq\boldsymbol{u}_k^T\boldsymbol{v}$实际上代表了夹角$\langle \boldsymbol{u}_k,\boldsymbol{v}\rangle$比夹角$\langle \boldsymbol{u}_j,\boldsymbol{v}\rangle$小
$\boldsymbol{u_j}^T\boldsymbol{v}=||\boldsymbol{u}_j||||\boldsymbol{v}||\cos\theta_j=||\boldsymbol{v}||\cos\theta_j$
这里偏好向量$\boldsymbol{u_j}$都是单位向量。因此有
$\begin{aligned}||\boldsymbol{v}||\cos\theta_j\leq||\boldsymbol{v}||\cos\theta_k\Longrightarrow\cos\theta_j\leq\cos\theta_k\Longrightarrow\theta_j\ge\theta_k\end{aligned}$
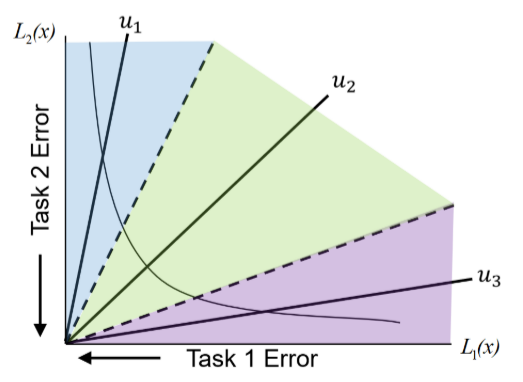
上图中虚线代表子区域的分隔线,其中绿色子区域$\Omega_2$中的任意向量$\boldsymbol{v}$与$\boldsymbol{u_2}$的夹角都更小。
因此子问题$p3$可以进一步表示为如下形式
$\begin{aligned}&\min_\theta\mathcal{L}(\theta)=(\mathcal{L}_1(\theta),\mathcal{L}_2(\theta),\cdots,\mathcal{L}_m(\theta))^T,\\& s.t.\quad\mathcal{G}_j(\theta_t)=(\boldsymbol u_j-\boldsymbol u_k)^T\mathcal L(\theta_t)\le 0,\forall j=1,\ldots,K,\end{aligned}\qquad (p4)$
这里约束条件$\mathcal{G}_j(\theta_t)$确保解$\theta_t$在目标空间中位于与偏好向量$\boldsymbol u_k$对应的子区域$\Omega_k$内。
梯度法求解子问题
寻找子区域内初始解
在优化问题中,优化起点一般是通过随机初始化神经网络参数得到一个随机生成的初始解$\theta_r$,然而该初始解$\theta_r$可能并不位于我们要求的子区域内,因此需要通过如下约束优化问题求得可行的初始解$\theta_0$
$\begin{aligned}&\min_{\theta_0}||\theta_0-\theta_r||^2\\&s.t.\quad\mathcal{L}(\theta_0)\in\Omega_k\end{aligned}$
然而,直接找到一个满足约束条件的初始解$\theta_0$是一个高维约束优化问题,尤其是在深度神经网络中,参数数量可能达到数百万,直接求解上述问题非常低效。为了提高效率,Lin等将该问题转化为一个多目标优化问题,并通过序列梯度下降法来找到可行初始解$\theta_0\;(\mathcal L(\theta_0)\in\Omega_k)$。
对于随机初始解$\theta_r$,首先定义所有激活约束的索引集合为
$I(\theta_r)=\{j|\mathcal G_j(\theta_r)\geq0,j=1,…,K\}$
$I(\theta_r)$中索引$j$代表解$\theta_r$不满足约束条件$\mathcal G_j$。$I(\theta_r)$表示了后续优化过程中需要被特别关注的约束,通过优化这些约束,可以使解$\theta_r$逐步满足所有约束条件,从而进入可行区域$\Omega_k$。
上述问题的优化目标是找到一个下降方向$d_r$,使得所有激活约束的值都能减少。这实际上就是一个多目标优化问题
$\begin{aligned}(d_r,\alpha_r)=&\arg\min_{d\in\mathbb R^n,\alpha\in\mathbb R}\alpha+\frac{1}{2}||d||^2\\ &s.t.\;\nabla \mathcal G_j(\theta_r)^Td\leq\alpha,j\in I(\theta_r)&\end{aligned}$
该多目标优化问题的求解可以通过上文提到的MGDA算法实现,找到一个位于子区域$\Omega_k$的初始解$\theta_r$。
求解子问题
当我们找到一个位于子区域内的初始解$\theta_r$后,可以通过梯度方法进一步找到子问题的帕累托最优解$\theta^*$。下面先给出偏好场景下受限帕累托最优的定义
$\textbf{定义. 受限帕累托最优(Restricted Pareto Optimality)}$ 若$\theta^*$是$\mathcal L(\theta)$在子区域$\Omega_k$中的帕累托最优点,则满足$\theta^*\in\Omega_k$且不存在$\hat\theta\in\Omega_k$使得$\hat{\theta}\prec\theta^*$。
基于上面的定义,我们可以将原子问题转化为如下的多目标约束优化问题
$\begin{aligned}
(d_t, \alpha_t) = &\arg\min_{d \in \mathbb{R}^n, \alpha \in \mathbb{R}} \alpha + \frac{1}{2} ||d||^2 \\
\text{s.t.} \quad & \nabla\mathcal{L}_i(\theta_t)^T d \leq \alpha, \quad i = 1, \dots, m. \\
& \nabla\mathcal{G}_j(\theta_t)^T d \leq \alpha, \quad j \in I_\epsilon(\theta_t),
\end{aligned}\qquad(p4)$
其中$I_{\epsilon}(\theta)$是子区域约束$I_{\epsilon}(\theta)=\{j\in I|\mathcal{G}_{j}(\theta)\geq-\epsilon\}$。$\epsilon$是一个小阈值,用于处理接近约束边界的解。
通过求解问题$p4$可以得到梯度下降方向$d_t$,根据求解结果可以分为如下两种情况
- 如果$d_t=0$,则表示当前解$\theta_t$是子区域$\Omega_k$中的一个帕累托稳定点
- 如果$d_t\neq0$,则$d_t$是一个有效的下降方向,可以同时减少所有任务损失和激活约束的值
形式化定义如下
$\textbf{引理 }$ 若$(d_t, \alpha_t)$是问题$p4$的解,则有满足情况
- 如果$\theta_t$是子区域$\Omega_k$中的帕累托稳定点,则满足$d_t=\mathbf{0}\in\mathbb{R}^n,\alpha_t=0$
- 如果$\theta_t$不是子区域$\Omega_k$中的帕累托稳定点,则满足
$\begin{aligned}&\alpha_{t}\leq-(1/2)||d_{t}||^{2}<0,\\&\nabla\mathcal{L}_{i}(\theta_{t})^{T}d_{t}\leq\alpha_{t},i=1,…,m\\&\nabla\mathcal{G}_{j}(\theta_{t})^{T}d_{t}\leq\alpha_{t},j\in I_{\epsilon}(\theta_{t}).\end{aligned}$
如果当前解$\theta_t$不是帕累托稳定点,那么可以通过梯度下降法更新解$\theta_{t+1}=\theta_t+\eta_td_t$。通过求解所有子问题,可以得到一组分布在目标空间不同子区域中的帕累托临界解。这些解代表了原始多任务学习问题中不同任务之间的权衡。
对偶优化
与传统的多重梯度下降类似,问题$p4$并不好直接求解,尤其是在神经网络参数维度较高的情况下。因此我们可以参考MGDA,利用问题$p4$的拉格朗日对偶问题的KKT条件进行求解,降低问题维度使其更适合大规模优化。问题$p4$的拉格朗日对偶问题如下
$\begin{aligned}&\max_{\lambda_{i},\beta_{j}}-\frac{1}{2}\left\|\sum_{i=1}^{m}\lambda_{i}\nabla\mathcal{L}_{i}(\theta_{t})+\sum_{j\in I_{\epsilon}({\theta}_t)}\beta_{i}\nabla\mathcal{G}_{j}(\theta_{t})\right\|^{2}\\&s.t.\quad\sum_{i=1}^{m}\lambda_{i}+\sum_{j\in I_{\epsilon}(\theta)}\beta_{j}=1,\lambda_{i}\geq0,\beta_{j}\geq0,\forall i=1,…,m,\forall j\in I_{\epsilon}(\theta).\end{aligned}\quad(p5)$
问题$p5$的KKT条件具体推导过程与多重梯度下降对偶问题类似,这里不再赘述。根据 KKT 条件,下降方向$d_t$如下
$\begin{aligned}&d_{t}=-\left(\sum_{i=1}^m\lambda_i\nabla\mathcal{L}_i(\theta_t)+\sum_{j\in I_\epsilon(\theta_t)}\beta_j\nabla \mathcal G_j(\theta_t)\right)\\&s.t.\;\sum_{i=1}^m\lambda_i+\sum_{j\in I_\epsilon(\theta)}\beta_j=1,\quad\lambda_i\ge0,\beta_i\ge0,\forall i=1,…,m,\forall j\in I_{\epsilon}(\theta)\end{aligned}$
原问题$p4$的决策空间是参数空间,维度可能高达数百万。而其对偶问题$p5$的决策空间是目标和约束空间,维度只有$m+|I_{\epsilon}(\theta_t)|$,其中$m$是子问题数,$|I_{\epsilon}(\theta_t)|$是激活约束的数量。由于对偶问题的维度显著降低,求解对偶问题的计算效率远高于原始问题。这使得 Pareto MTL 算法能够高效地处理大规模优化问题。
此外,Pareto MTL 算法的所有子问题可以并行求解,因为在优化过程中子问题之间没有数据相关。每个子问题的唯一偏好信息是偏好向量集。在没有先验知识的情况下,默认的偏好向量是均匀分布的。例如,对于 2 个任务,可以选择$K+1$个偏好向量,这些偏好向量将目标空间均匀划分为不同的子区域,确保生成的解具有不同的权衡。
$\begin{aligned}\left\{\left(\cos\left(\frac{k\pi}{2K}\right),\sin\left(\frac{k\pi}{2K}\right)\right)\middle|k=0,1,\ldots,K\right\}\end{aligned}$
Pareto MTL算法流程如下
- 算法名称:$\textbf{Pareto MTL}$
- 算法输入:均匀初始化的偏好向量集$\{{u_{1},u_{2},…,u_{K}}\}$
- 算法输出:一组带有不同权衡的子问题解集$\{\theta_{T}^{(k)}|k=1,\ldots,K\}$
- 算法流程:(可并行)
- $\textbf{for }k=1 \text{ to }K \textbf{ do}$
- $\quad$随机初始化子问题$k$的初始解$\theta_r^{(k)}$
- $\quad$使用梯度下降基于$\theta_r^{(k)}$寻找可行初始解初始解$\theta_0^{(k)}$
- $\quad\textbf{for }k=1 \text{ to }T \textbf{ do}\qquad T\text{看作梯度下降循环条件}$
- $\qquad$使用MGDA求解问题$p5$得到一组权重$\lambda_{ti}^{(k)}\geq0,\beta_{ti}^{(k)}\geq0,\forall i=1,…,m,\forall j\in I_{\epsilon}(\theta)$
- $\qquad$基于权重计算更新方向$d_{t}^{(k)}=-(\sum_{i=1}^{m}\lambda_{ti}^{(k)}\nabla\mathcal{L}_{i}(\theta_{t}^{(k)})+\sum_{j\in I_{\epsilon(x)}}\beta_{ti}^{(k)}\nabla\mathcal{G}_{j}(\theta_{t}^{(k)}))$
- $\qquad$更新参数$\theta_{t+1}^{(k)}=\theta_{t}^{(k)}+\eta d_{t}^{(k)}$
- $\quad\textbf{end for}$
- $\textbf{end for}$
Pareto MTL与MOO-MTL
Pareto MTL是从多目标优化MOO角度提出的,与多任务下的MGDA类似,Pareto MTL也可以被形式化为一种自适应线性标量化方法。
首先考虑一种无约束的情况,即不进行子问题分解并移除所有约束条件,则Pareto MTL的更新规则将退化为 MGDA的更新规则,多任务学习的线性标量化形式如下
$\mathcal{L}(\theta_t)=\sum_{i=1}^m\lambda_i\mathcal{L}_i(\theta_t),$
其对偶问题如下
$\begin{aligned}&\max_{\lambda_{i}}-\frac{1}{2}\left\|\sum_{i=1}^{m}\lambda_{i}\nabla\mathcal{L}_{i}(\theta_{t})\right\|^{2},\\&s.t.\sum_{i=1}^{m}\lambda_{i}=1,\quad\lambda_{i}\geq0,\forall i=1,…,m.\end{aligned}$
此时我们再引入Pareto MTL 算法中了额外的约束项$\mathcal{G}_j(\theta_t)$。如果约束被激活,则可以忽略。如果约束被激活,假设对应子问题的偏好向量是$\boldsymbol{u}_k$,则有
$\nabla\mathcal{G}_j(\theta_t)=(\boldsymbol{u}_j-\boldsymbol{u}_k)^T\nabla\mathcal{L}(\theta_t)=\sum_{i=1}^m(\boldsymbol{u}_{ji}-\boldsymbol{u}_{ki})\nabla\mathcal{L}_i(\theta_t)$
因此Pareto MTL 算法可以被重新形式化为
$\begin{aligned}&\mathcal{L}(\theta_t)=\sum_{i=1}^m\alpha_i\mathcal{L}_i(\theta_t),\\&\mathrm{where}\;\alpha_i=\lambda_i+\sum_{j\in I_{\epsilon(\theta)}}\beta_j(\boldsymbol{u}_{ji}-\boldsymbol{u}_{ki})\end{aligned}$
其中拉格朗日乘子$\lambda_i,\beta_i$是通过求解问题$p5$得到的。MOO-MTL和 Pareto MTL 都是从多目标优化的角度提出的,但它们也可以被视为自适应线性标量化方法。
- MOO-MTL 通过平衡不同任务的梯度来找到一个帕累托最优解
- Pareto MTL 通过分解多目标问题为多个子问题,并引入偏好向量来生成一组具有不同权衡的帕累托最优解
相比于MOO-MTL,Pareto MTL 中的自适应权重$\alpha_i$不仅考虑了任务的损失函数$\mathcal{L}_i(\theta_t)$,还考虑了约束条件$\mathcal{G}_j(\theta_t)$,这使得Pareto MTL 算法能够生成一组具有不同权重的Pareto最优解。
原论文中Synthetic Example部分的Pareto MTL算法实现核心代码如下
# use autograd to calculate the gradient
import autograd.numpy as np
from autograd import grad
from matplotlib import pyplot as plt
### functions for solving QP problem ###
# can use cvxopt or use the min_norm_solvers written by the author of MOO-MTL
#cvxopt是一个开源的Python库,专门用于解决凸优化问题。它提供了丰富的工具和函数,可以高效地求解线性规划(LP)、二次规划(QP)、半定规划(SDP)以及二次约束规划(QCP)等多种优化问题
#import cvxopt
#from cvxopt import matrix
#定义了一个函数 cvxopt_solve_qp,用于求解二次规划问题
#MGDA实际上是一个带有线性约束的凸二次型问题
#P 和 q 是二次规划问题的标准形式中的矩阵和向量,用于定义目标函数
#G 和 h 是不等式约束的矩阵和向量
#A 和 b 是等式约束的矩阵和向量
#def cvxopt_solve_qp(P, q, G=None, h=None, A=None, b=None):
#确保矩阵 P 是对称的
# P = .5 * (P + P.T) # make sure P is symmetric
# 将矩阵 P 和向量 q 的数据类型转换为 np.double
# P = P.astype(np.double)
# q = q.astype(np.double)
# 创建一个列表 args,并将矩阵 P 和向量 q 转换为 cvxopt.matrix 类型
# args = [matrix(P), matrix(q)]
# 这里使用了 extend 方法,将多个参数动态地添加到 args 列表中
# if G is not None:
# args.extend([matrix(G), matrix(h)])
# if A is not None:
# args.extend([matrix(A), matrix(b)])
#调用 cvxopt.solvers.qp 函数,传入 args 列表中的所有参数,求解二次规划问题
# sol = cvxopt.solvers.qp(*args)
# 检查求解器返回的状态
# if 'optimal' not in sol['status']:
# return None
# 这里假设解是一个向量,其长度等于矩阵 P 的列数
# return np.array(sol['x']).reshape((P.shape[1],))
from min_norm_solvers_numpy import MinNormSolver
#用于计算多目标优化(Multi-Objective Optimization, MOO)中的梯度方向
#输入参数是 grads,表示多个任务的梯度
#MGDA
def get_d_moomtl(grads):
"""
calculate the gradient direction for MOO-MTL
"""
#nobj 表示任务的数量(即梯度的数量),dim 表示每个梯度的维度(即模型参数的数量)
nobj, dim = grads.shape
# # use cvxopt to solve QP
#计算矩阵 P,它是梯度矩阵 grads 与其转置的乘积,即M
# P = np.dot(grads , grads.T)
# 定义向量 q,其长度为任务数量 nobj,并初始化为全零,在二次规划问题中,q 是目标函数的线性项系数向量
# q = np.zeros(nobj)
# G 是一个负单位矩阵,表示每个任务的权重必须非负,h 是一个全零向量,与 G 一起表示不等式约束
# G = - np.eye(nobj)
# h = np.zeros(nobj)
#
# A 是一个全一矩阵,表示任务权重的和为 1,b 是一个全一向量,与 A 一起表示约束条件
# A = np.ones(nobj).reshape(1,2)
# b = np.ones(1)
#
# cvxopt.solvers.options['show_progress'] = False
# sol = cvxopt_solve_qp(P, q, G, h, A, b)
# use MinNormSolver to solve QP
sol, nd = MinNormSolver.find_min_norm_element(grads)
#返回计算得到的任务权重最优解 sol
return sol
#Pareto MLT算法
#带偏好向量的MGDA
def get_d_paretomtl(grads,value,weights,i):
# calculate the gradient direction for Pareto MTL
nobj, dim = grads.shape
# check active constraints
#偏好向量处理
normalized_current_weight = weights[i]/np.linalg.norm(weights[i])
normalized_rest_weights = np.delete(weights, (i), axis=0) / np.linalg.norm(np.delete(weights, (i), axis=0), axis = 1,keepdims = True)
w = normalized_rest_weights - normalized_current_weight
# solve QP
##相当于计算G_j(\theta_t)
gx = np.dot(w,value/np.linalg.norm(value))
idx = gx > 0
#通过拼接梯度矩阵 grads 和活跃约束对应的加权梯度,构造新的向量 vec
#######这里约束的增加是通过拼接梯度得到的#######
vec = np.concatenate((grads, np.dot(w[idx],grads)), axis = 0)
# # use cvxopt to solve QP
#
# P = np.dot(vec , vec.T)
#
# q = np.zeros(nobj + np.sum(idx))
#
# G = - np.eye(nobj + np.sum(idx) )
# h = np.zeros(nobj + np.sum(idx))
#
#
#
# A = np.ones(nobj + np.sum(idx)).reshape(1,nobj + np.sum(idx))
# b = np.ones(1)
# cvxopt.solvers.options['show_progress'] = False
# sol = cvxopt_solve_qp(P, q, G, h, A, b)
# use MinNormSolver to solve QP
#得到一个▽L和▽g都下降的方向
sol, nd = MinNormSolver.find_min_norm_element(vec)
# sol×▽g=sol×w×▽L=sol×w×▽L1+sol×w×▽L2
#sol+sol×▽g
# reformulate ParetoMTL as linear scalarization method, return the weights
weight0 = sol[0] + np.sum(np.array([sol[j] * w[idx][j - 2,0] for j in np.arange(2,2 + np.sum(idx))]))
weight1 = sol[1] + np.sum(np.array([sol[j] * w[idx][j - 2,1] for j in np.arange(2,2 + np.sum(idx))]))
weight = np.stack([weight0,weight1])
return weight
#计算 Pareto 多任务学习(MTL)初始化阶段的梯度方向
#梯度矩阵 grads、目标值 value、偏好向量矩阵 weights 和偏好向量索引 i
def get_d_paretomtl_init(grads,value,weights,i):
# calculate the gradient direction for Pareto MTL initialization
nobj, dim = grads.shape
# check active constraints
#计算当前任务(索引为 i)的偏好向量 weights[i] 的归一化形式。归一化是为了确保偏好向量的长度为1,这有助于后续计算中保持数值稳定性和一致性。
normalized_current_weight = weights[i]/np.linalg.norm(weights[i])
#计算除第 i 个偏好向量外其他所有偏好向量的归一化形式。这里使用 np.delete 函数从 weights 中删除第 i 行,然后对剩余的偏好向量进行归一化处理
normalized_rest_weights = np.delete(weights, (i), axis=0) / np.linalg.norm(np.delete(weights, (i), axis=0), axis = 1,keepdims = True)
#计算其他偏好向量与第 i 个偏好向量的差值 w。这个差值向量 w 用于后续的激活约束检查,帮助确定哪些约束在当前偏好向量下是活跃的
#相当于计算G_j(\theta_t)
w = normalized_rest_weights - normalized_current_weight
#计算偏好向量差值 w 与归一化目标值 value 的点积 gx。点积的结果用于评估每个约束的活跃状态,
#这里实际上是一个子区域对应一组约束
#对应子区域,其符号实际上有[-,-,-,...,0,...,-]
#只有u_k的值为0,其余的值都为负时,说明解落在子区域k内了
gx = np.dot(w,value/np.linalg.norm(value))
#求激活约束I(\theta_r),idx代表解不满足约束条件
idx = gx > 0
#全负说明没有偏好向量
if np.sum(idx) <= 0:
return np.zeros(nobj)
#如果只有一个活跃约束(即 idx 中只有一个元素为 True),则返回一个全一向量。这表示在当前偏好向量下,只有一个约束需要特别关注,因此可以直接返回一个全一向量作为解。
#说明解落在了偏好区域内了
if np.sum(idx) == 1:
#只有一个梯度,权重直接返回全1
sol = np.ones(1)
#说明解位于偏好区域内,需要梯度下降找到一个位于偏好区域内的解
else:
#如果有多个活跃约束(即 idx 中有多个元素为 True),则需要通过梯度下降减小约束gx的值,直到所有gx为负数
#gx的梯度,等于差值u×l的梯度
vec = np.dot(w[idx],grads)
#求解使约束gx梯度同时下降的方向和值大小
sol, nd = MinNormSolver.find_min_norm_element(vec)
# calculate the weights
#这里是如何将gx的权重转换成L的权重???
#g=w×L
#▽g=w×▽L
#sol×▽g=sol×w×▽L=sol×w×▽L1+sol×w×▽L2
#根据最小范数解 sol 和活跃约束的偏好向量差值 w[idx],计算最终的任务权重 weight
weight0 = np.sum(np.array([sol[j] * w[idx][j ,0] for j in np.arange(0, np.sum(idx))]))
weight1 = np.sum(np.array([sol[j] * w[idx][j ,1] for j in np.arange(0, np.sum(idx))]))
weight = np.stack([weight0,weight1])
return weight
#生成偏好向量
def circle_points(r, n):
# generate evenly distributed preference vector
circles = []
for r, n in zip(r, n):
t = np.linspace(0, 0.5 * np.pi, n)
x = r * np.cos(t)
y = r * np.sin(t)
circles.append(np.c_[x, y])
return circles
### the synthetic multi-objective problem ###
def f1(x):
n = len(x)
sum1 = np.sum([(x[i] - 1.0/np.sqrt(n)) ** 2 for i in range(n)])
f1 = 1 - np.exp(- sum1)
return f1
def f2(x):
n = len(x)
sum2 = np.sum([(x[i] + 1.0/np.sqrt(n)) ** 2 for i in range(n)])
f2 = 1 - np.exp(- sum2)
return f2
# calculate the gradients using autograd
f1_dx = grad(f1)
f2_dx = grad(f2)
def concave_fun_eval(x):
"""
return the function values and gradient values
"""
return np.stack([f1(x), f2(x)]), np.stack([f1_dx(x), f2_dx(x)])
### create the ground truth Pareto front ###
def create_pf():
ps = np.linspace(-1/np.sqrt(2),1/np.sqrt(2))
pf = []
for x1 in ps:
#generate solutions on the Pareto front:
x = np.array([x1,x1])
f, f_dx = concave_fun_eval(x)
pf.append(f)
pf = np.array(pf)
return pf
### optimization method ###
def linear_scalarization_search(t_iter = 100, n_dim = 20, step_size = 1):
"""
linear scalarization with randomly generated weights
"""
r = np.random.rand(1)
weights = np.stack([r, 1-r])
x = np.random.uniform(-0.5,0.5,n_dim)
for t in range(t_iter):
#返回f的值和梯度
f, f_dx = concave_fun_eval(x)
x = x - step_size * np.dot(weights.T,f_dx).flatten()
return x, f
def moo_mtl_search(t_iter = 100, n_dim = 20, step_size = 1):
"""
MOO-MTL
"""
x = np.random.uniform(-0.5,0.5,n_dim)
for t in range(t_iter):
f, f_dx = concave_fun_eval(x)
weights = get_d_moomtl(f_dx)
x = x - step_size * np.dot(weights.T,f_dx).flatten()
return x, f
def pareto_mtl_search(ref_vecs,i,t_iter = 100, n_dim = 20, step_size = 1):
"""
Pareto MTL
"""
# print(ref_vecs)
# randomly generate one solution
#生成一个初始的20维的解
x = np.random.uniform(-0.5,0.5,n_dim)
#先找到一个位于偏好子区域内的初始解
# find the initial solution
for t in range(int(t_iter * 0.2)):
# 返回初始点f的值和梯度
f, f_dx = concave_fun_eval(x)
weights = get_d_paretomtl_init(f_dx,f,ref_vecs,i)
# print(weights)
x = x - step_size * np.dot(weights.T,f_dx).flatten()
# find the Pareto optimal solution
for t in range(int(t_iter * 0.8)):
f, f_dx = concave_fun_eval(x)
weights = get_d_paretomtl(f_dx,f,ref_vecs,i)
# print(weights)
x = x - step_size * np.dot(weights.T,f_dx).flatten()
return x, f
def run(method = 'ParetoMTL', num = 10):
"""
run method on the synthetic example
method: optimization method {'ParetoMTL', 'MOOMTL', 'Linear'}
num: number of solutions
"""
#生成pareto前沿
pf = create_pf()
f_value_list = []
weights = circle_points([1], [num])[0]
print(weights)
for i in range(num):
print(i)
if method == 'ParetoMTL':
x, f = pareto_mtl_search(ref_vecs = weights,i = i)
if method == 'MOOMTL':
x, f = moo_mtl_search()
if method == 'Linear':
x, f = linear_scalarization_search()
f_value_list.append(f)
f_value = np.array(f_value_list)
plt.plot(pf[:,0],pf[:,1])
plt.scatter(f_value[:,0], f_value[:,1], c = 'r', s = 80)
plt.show()
run('ParetoMTL')基于偏好MGDA的ATL
辅助任务学习(Auxiliary Task Learning, ATL)是一种多任务学习方法,旨在通过引入辅助任务来提升主任务的性能。其核心思想是,通过同时学习多个相关任务,模型能够共享特征表示,从而提高泛化能力和学习效率。如在图像分类中,主任务是分类任务,辅助任务可以是图像分割任务。通过同时学习这两个任务,模型能够更好地理解图像内容,从而提高分类准确率。
Pareto MTL算法通过引入偏好向量来生成一组具有不同权衡的Pareto最优解,在此基础上,Chen等人提出了一种针对少样本辅助任务学习的PSST(Pareto self-supervised training)算法,基于偏好向量进一步提升模型在主任务上的性能。
在少样本辅助任务学习中,重点在于在从多个任务中找到主任务性能最佳的偏好区域。PSST采用的方法是排除那些对主任务性能不利的区域,该区域主任务的性能比平衡主任务性能差。
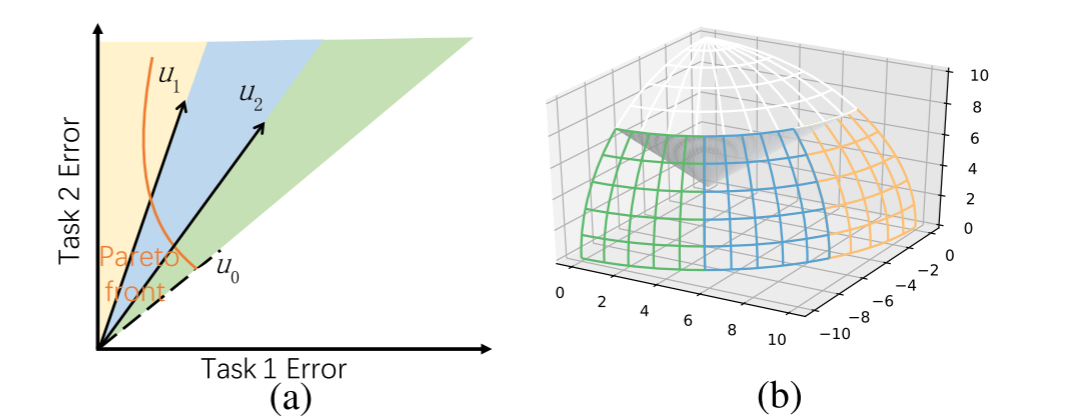
如上图$(a)$是两任务的情况,其中$\text{Task 1}$是主任务,$u_0$是任务1和2平衡区域的偏好向量。PSST移除了位于$u_0$下方的区域,在该区域$\text{Task 1}$的性能比剩余区域中$\text{Task 1}$的性能更差。$(b)$是三任务的情况,同理白色区域是被移除的子区域。
主任务性能比例
作者假设,当所有任务的性能达到平衡时,多任务模型整体性能最佳。如果主任务的性能比主任务的平衡性能差,则称辅助任务阻碍了主任务。论文引入了一个关键指标任务性能比例$\rho(\theta)$表示主任务性能与所有辅助任务性能的比例
$\begin{aligned}\rho(\theta)=\frac{\mathcal L_1(\theta)}{\sum_{m=2}^M\mathcal L_m(\theta)}\end{aligned}$
其中$\mathcal L_1(\theta)$是主任务的损失函数,$\mathcal L_m(\theta)$是第$m$个辅助任务的损失函数。基于该定义,论文提出了如下引理
$\textbf{引理 1. }$若解$\theta^*_{\pi0}$达到了整体最佳性能,即$\min_{\theta}\;\sum_{m=1}^M\mathcal L_m(\theta)=\sum_{m=1}^M\mathcal L_m(\theta^*_{\pi0})$,解$\theta^\prime$在主任务上有更好的性能$\mathcal L_1(\theta^\prime)<\mathcal L_1(\theta^*_{\pi0})$,则满足
$\rho(\theta^\prime)<\rho(\theta^*_{\pi0})$
这里$\rho(\theta)=\rho(\theta^*_{\pi0})$是PSST用于分割两部分区域的超平面。PSST移除了辅助任务阻碍主任务的部分$\rho(\theta)>\rho(\theta^*_{\pi0})$,而$\rho(\theta)\le\rho(\theta^*_{\pi0})$部分区域中主任务的性能优于或等于平衡性能,因此是后续优化过程中需要关注的部分。然后该区域部分进一步使用偏好向量分割来避免残差错误积累。引理1的证明如下
首先由反证法引出,当$L_1(\theta^{\prime})<L_1(\theta_{\pi0}^*)$成立时,假设下式也成立
$\sum_{m=2}^ML_m(\theta^{\prime})<\sum_{m=2}^ML_m(\theta_{\pi0}^*)$
则有
$\sum_{m=1}^ML_m(\theta^{\prime})<\sum_{m=1}^ML_m(\theta_{\pi0}^*)=min_\theta\sum_{m=1}^ML_m(\theta).$
然而$\theta_{\pi0}^*$已是整体性能最佳的Pareto最优解,不可能存在解$\theta^\prime$比解$\theta_{\pi0}^*$更优,因此假设不成立。故当$L_1(\theta^{\prime})<L_1(\theta_{\pi0}^*)$成立时,下式成立
$\sum_{m=2}^{M}L_{m}(\theta^{\prime})>\sum_{m=2}^{M}L_{m}(\theta_{\pi0}^{*})$
因此最终有$\rho(\theta^\prime)<\rho(\theta^*_{\pi0})$成立
$\begin{aligned}\rho(\theta^{\prime})&=\frac{L_{1}(\theta^{\prime})}{\sum_{m=2}^{M}L_{m}(\theta^{\prime})}\\&<\frac{L_1(\theta_{\pi0}^*)}{\sum_{m=2}^ML_m(\theta^{\prime})}\\&<\frac{L_{1}(\theta_{\pi0}^{*}))}{\sum_{m=2}^{M}L_{m}(\theta_{\pi0}^{*}))}\\&=\rho(\theta_{\pi0}^{*}).\end{aligned}$
子任务分解
对于平衡解$\theta^*_{\pi0}$来说有$\mathcal{L}(\theta_{\pi0}^*)=[\mathcal{L}_{1}(\theta_{\pi0}^*),\mathcal{L}_{2}(\theta_{\pi0}^*),\cdots,\mathcal{L}_{M}(\theta_{\pi0}^*)]^{\mathrm{T}}$。这里$\rho(\theta^*_{\pi0})$可以看作是一个分割主任务性能的超平面,我们重点关注主任务更优的$\rho(\theta^\prime)<\rho(\theta^*_{\pi0})$区域。PSST的子任务分解,在主任务更优区域中,使用偏好向量对这一区域进行均匀划分来进一步分解子任务区域。
以两任务场景为例,坐标平面是二维空间,对应的分割主任务性能的$\rho(\theta)=\rho(\theta^*_{\pi0})$是一条直线,对应的方向方向是$u_0=(\cos\pi_0,\sin\pi_0)$,其中
$\begin{aligned}\cos\pi_{0}=\frac{e_{1}\mathcal{L}(\theta_{\pi0}^{*})}{\left\|T_{2}\mathcal{L}(\theta_{\pi0}^{*})\right\|_{2}}\end{aligned}$
这里$e^{mm}$是单入口矩阵,第$m$行$m$列的元素为$1$其余为$0$,$T_{m}=I-e^{mm}$,$I$是单位矩阵,如$e_1=(1,0)^T$。
给定$u_0$,进一步将辅助问题分解为$K$个子问题,每个子问题对应一个单位偏好向量$\{{u_{1},u_{2},…,u_{K}}\}$,其中每个偏好向量$u_i$的形式为
$\begin{aligned}&u_{i}=\left(\cos\pi_{i},\sin\pi_{i}\right)\\&s.t.\;\pi_{i}=\frac{i}{K}\left(\frac{\pi}{2}-\pi_{0}\right)+\pi_{0},\;i=1,\ldots,K\end{aligned}$
这里的$\pi_i$是通过均匀分割主偏好区间角度得到的,确保每个子问题在偏好区域内进行探索。为了确保在偏好区域内找到Pareto最优解,下面将每个子问题转换成约束条件,确保解落在特定的偏好区域内。
假设所有目标函数都是非负的,则对应于偏好向量$u_i$和$u_{i+1}$之间的多目标子问题可以表示为
$\begin{aligned}&\min_{\theta}\mathcal{L}(\theta)=\left(\mathcal{L}_{1}(\theta),\mathcal{L}_{2}(\theta),\cdots,\mathcal{L}_{M}(\theta)\right)^{\mathrm{T}}\\&s.t.\;u_{i}e_{1}{}^{T}\leq\frac{e_{1}\mathcal{L}(\theta)}{||T_{2}\mathcal{L}(\theta)||_{2}}\leq u_{i+1}e_{1}{}^{T}.\end{aligned}$
这里$e_1$是单位向量,$T_2$是投影矩阵用于将损失向量投影到特定的子空间。上述子问题可以进一步重写为如下形式
$\begin{aligned}\min_{\theta}\;&\mathcal{L}(\theta)=\left(\mathcal{L}_{1}(\theta),\mathcal{L}_{2}(\theta),\cdots,\mathcal{L}_{M}(\theta)\right)^{\mathrm{T}}\\s.t.\;&\mathcal{Q}_{i}(\theta)=\frac{e_{1}\mathcal{L}(\theta)}{\left\|T_{2}\mathcal{L}(\theta)\right\|_{2}}-u_{i+1}e_{1}{}^{T}\leq0,\\&\mathcal{R}_{i}(\theta)=u_{i}{e_{1}}^{T}-\frac{e_{1}\mathcal{L}(\theta)}{\left\|T_{2}\mathcal{L}(\theta)\right\|_{2}}\leq0.\end{aligned}$
偏好Pareto最优
与Pareto MTL类似,要解决带偏好向量$u_i$和$u_{i+1}$的MOO约束子问题,可以从其对偶问题入手。激活约束表示为$\mathcal{K}_{\epsilon}(\theta)=\{k|\mathcal{Q}_{k}(\theta)\geq-\epsilon,k=0,\ldots,K-1\}$和$\mathcal{J}_{\epsilon}(\theta)=\{j|\mathcal{R}_{j}(\theta)\geq-\epsilon,j=0,\ldots,K-1\}$,其中$\epsilon$代表门限值。由此带约束的原问题可以表示成如下
$\begin{aligned}(d_{t},\alpha_{t})=&\arg\min_{d\in R^{M},\alpha\in R}\alpha+\frac{1}{2}\|d\|^{2},\\\mathrm{s.t.}\;&\nabla\mathcal{L}_{m}\left(\theta_{t}\right)^{T}d\leq\alpha,m=1,\ldots,M.\\&\nabla\mathcal{Q}_{k}(\theta_{t})^{T}d\leq\alpha,k\in\mathcal{K}_{\epsilon}(\theta_{t}),\\&\nabla\mathcal{R}_{j}(\theta_{t})^{T}d\leq\alpha,j\in\mathcal{J}_{\epsilon}(\theta_{t}).\end{aligned}$
其对偶问题可以表示成如下形式
$\begin{aligned}&\max_{\omega_{m},\beta_{k},\gamma_{j}}-\frac{1}{2}\left\|d_{t}\left(\omega_{m},\beta_{k},\gamma_{j}\right)\right\|^{2},\\&{s.t.}\sum_{m=1}^{M}\omega_{m}+\sum_{k\in\mathcal{K}_{\epsilon}(\theta_{t})}\beta_{k}+\sum_{j\in\mathcal{J}_{\epsilon}(\theta_{t})}\gamma_{j}=1,\\&\qquad\forall m=1,\ldots,M,\forall k\in\mathcal{K}_{\epsilon}(\theta_{t}),\forall j\in\mathcal{J}_{\epsilon}(\theta_{t}),\\&\qquad\omega_{m}\geq0,\beta_{k}\geq0,\gamma_{j}\geq0.\end{aligned}\qquad(p6)$
下降方向$d_t$可以通过其对偶问题$p6$的KKT条件求得
$d_{t}\left(\omega_{m},\beta_{k},\gamma_{j}\right)=-\left(\sum_{m=1}^{M}\omega_{m}\nabla\mathcal{L}_{m}\left(\theta_{t}\right)+\sum_{k\in\mathcal{K}_{\epsilon}(\theta_{t})}\beta_{k}\nabla\mathcal{Q}_{k}\left(\theta_{t}\right)+\sum_{j\in\mathcal{J}_{\epsilon}(\theta_{t})}\gamma_{j}\nabla\mathcal{R}_{j}(\theta_{t})\right)$
Pareto偏好搜索
帕累托搜索的目标是找到多个帕累托解。与传统的加权求和法相比,帕累托搜索在寻找帕累托解时更加高效。然而传统的帕累托搜索存在残差误差累积的问题,作者通过在子区域中搜索减少误差累积。
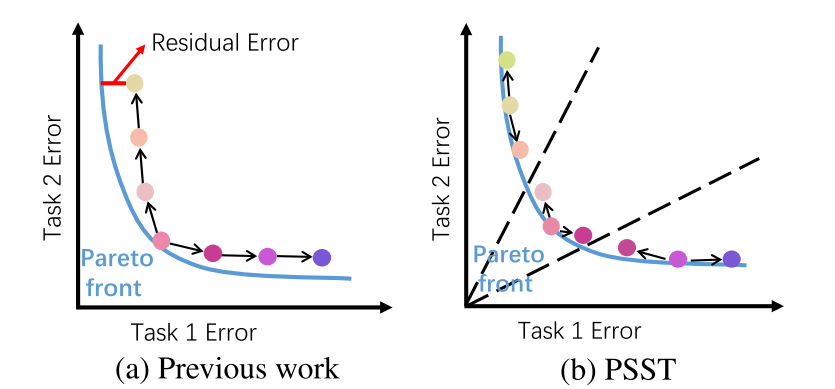
首先以一个初始随机解$\theta$作为参数,并通过上文的$d_t$作为下降方向得到一个Pareto解$\theta^*$。接着通过在解切平面上生成新的点$\theta_t$来探索其局部帕累托集。
$\textbf{引理 }$如果$\theta^*$是帕累托最优的,那么存在一个$\lambda\in\mathbb{R}^M$满足
$\lambda_m\geq0,\quad\sum_{m=1}^M\lambda_m=1,\quad\sum_{m=1}^M\lambda_m\nabla L_m(\theta^*)=0$
$\textbf{命题 }$假设$\mathcal{L}(\theta^*)$是光滑的,并且$\theta^*$是帕累托最优的。考虑任何在帕累托集中且通过$\theta^*$的光滑曲线$\theta(x)$:$(-\epsilon,\epsilon)\to\mathbb{R}^{M}$,即$\theta(0)=\theta^*$,那么存在一个$\beta\in\mathbb{R}^{M}$使得:
$H\left(\theta^*\right)\frac{d\theta}{dx}(0)=\nabla\mathcal{L}\left(\theta^*\right)^\top\beta$
其中$\mathrm{H}(\theta^{*})=\sum_{m=1}^{M}\lambda_{m}\nabla^{2}\mathcal{L}_{m}\left(\theta^{*}\right)$是Hessian矩阵,$\frac{d\theta}{dx}(0)$用于$\theta_{(0)}$点处的更新方向$\theta_{1}=\theta_{(0)}+\eta\frac{d\theta}{dx}(0)$。
为了解决上述矩阵求解问题,这里使用Krylov 子空间迭代方法。这种方法可以高效地求解大规模线性方程组,适用于高维优化问题。
生成一组偏好Pareto解
为了在偏好向量$u_i$和$u_{i+1}$定义的区域内探索一组帕累托解,首先初始化一个队列$q$和一个集合$s$,并将初始的帕累托解$\theta^*$加入队列和集合中
$q\leftarrow[\theta^*],\quad s\leftarrow[\theta^*]$
给定一个帕累托解$\theta^*$,可以在切平面上生成新的点$\theta_1$
$\begin{aligned}\theta_1=\theta^*+\eta\frac{d\theta}{dx}(0)\end{aligned}$
其中$\eta$是步长,$\frac{d\theta}{dx}(0)$是切平面上的梯度方向,用于更新参数。这里的$\theta_1$是$\theta^*$附近的一个一阶近似帕累托解。然后通过方向$d_t$找到一个精确的帕累托解$\theta^*_1$。然后将新找到的帕累托解$\theta^*_1$加入$q$和$s$
$q\leftarrow[\theta_1^*],\quad s\leftarrow[\theta_1^*]$
如果在$\theta^*$处无法找到任何近似点,我们将$\theta^*$从队列$q$中移除,并对队列中的所有点依次执行上面相同的操作。通过这种方式,我们可以在$u_i$和$u_{i+1}$定义的偏好区域内探索所有的帕累托解。
所有区域内的帕累托解都保存在集合$s$中。最终,选择在主任务中性能最好的帕累托解作为特定少样本任务的最终解。这里获取一个切平面方向的时间复杂度为$O(kn)$,$k$是迭代次数,$n$是输入数据的大小,由于时间复杂度与网络大小成线性关系,因此PSST 算法在大规模网络中仍然具有较高的效率。
- 算法名称:$\textbf{PSST}$
- 算法输入:随机初始化的神经网络参数$\theta$
- 算法输出:所有子问题解集$\{\boldsymbol{s}_{i}\mid i=1,\cdots,K\}$
- 算法流程:
- $使用\textbf{MOO-MTL}$算法找到一个初始平衡解$\theta^*_{\pi0}$
- 寻找主任务分割角度以及分割方向向量$\pi_{0}=\operatorname{arccos}\frac{e_{1}\mathcal{L}(\theta_{\pi0}^{*})}{\left|T_{2}\mathcal{L}(\theta_{\pi0}^{*})\right|_{2}},u_{0}=(\cos\pi_{0},\sin\pi_{0})$
- 计算主偏好区域内的偏好向量$\{\boldsymbol{u}_{1},\boldsymbol{u}_{2},\ldots,\boldsymbol{u}_{K}\}$
- $\textbf{for }i=0 \text{ to }K-1 \textbf{ do}$
- $\quad$随机生成参数$\theta^{(i)}$
- $\quad$基于$p6$的KKT条件得到的下降方向$d_t$求得主偏好区域内的一个解$\theta^{(i)*}$
- $\quad$使用$\textbf{PreferredParetoExploration}$算法得到一组具有不同权衡的主偏好Pareto解
- $\textbf{end for}$
基于冲突优化的梯度下降CAGrad
梯度冲突
在多任务学习中,不同任务的梯度之间可能存在冲突,梯度的大小和方向可能都不同。直接优化平均梯度方案可能导致某些任务的梯度被忽略,从而影响该任务性能。例如,当模型梯度接近一个陡峭的“山谷”时,某个任务的梯度可能主导更新,导致优化器在山谷中反复跳跃而无法更新参数。如下图的Adam情况
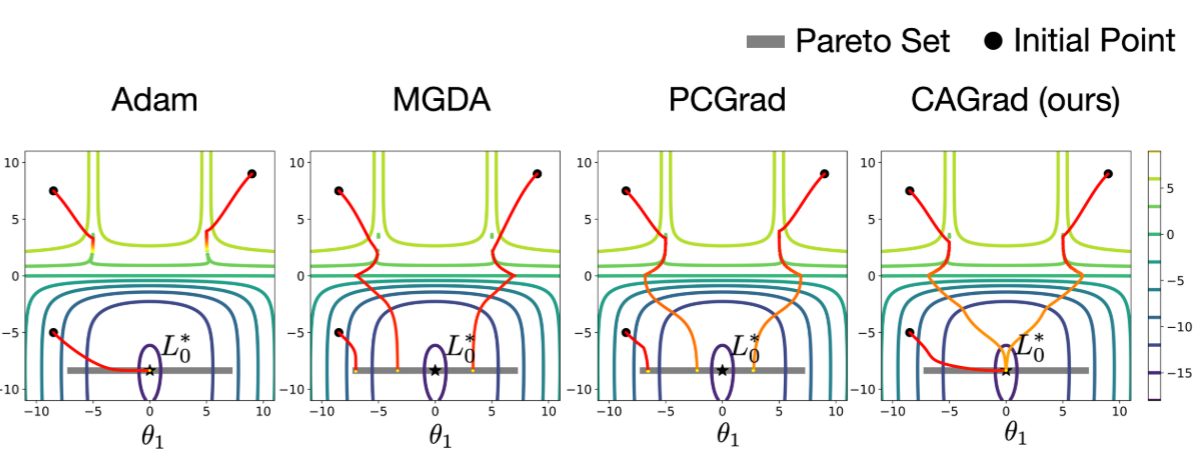
为了解决梯度冲突问题,现有方法主要通过动态调整任务权重或操纵梯度来改善优化过程,即优化损失和优化梯度。然而这些方法通常缺乏收敛保证,或者只能收敛到目标的任意帕累托稳定点,而无法保证收敛到最优解。
在多任务学习中,给定$K\le 2$个任务,每个任务对应的损失函数为$L_i(\theta)$其中$\theta$为任务共享参数。多任务学习的目标是找到一个最优解$\theta\in\mathbb R^m$,使得所有任务损失都较低。在实践中,MTL的一个标准目标是最小化所有任务的平均损失:
$\begin{aligned}\theta^*=\arg\min_{\theta\in \mathbb R^m}\left\{L_0(\theta)=\frac 1K\sum_{i=1}^K L_i(\theta)\right\}\end{aligned}$
然而,如果直接针对任务平均损失进行优化,可能会导致某些单任务的性能下降,这也称之为“跷跷板”现象。造成这一现象的主要原因就是——梯度冲突。具体来说,假如第$i$个任务的梯度表示为$g_i=\nabla L_i(\theta)$,平均梯度为$g_0=\nabla L_0(\theta)=\frac 1K\sum_{i=1}^K g_i$。在学习率$\alpha\in\mathbb R^+$下,针对平均梯度的参数下降更新可以表示为$\theta\leftarrow\theta-\alpha g_0$。然而,平均梯度的方向可能和单任务梯度方向冲突即$\exists i,\langle g_{i},g_{0}\rangle<0$,此时梯度下降实际上会降低任务$i$的性能。
当参数$\theta$接近一个陡峭的“山谷”时,特定任务的梯度将主导更新过程,导致某些任务梯度被忽略。因此操纵$g_0$的方向和大小来跳出山谷,通常可以带来更好的优化效果。具体来说,当$\theta$接近一个特定任务的梯度主导更新的区域时,调整$g_0$的方向和大小可以避免梯度冲突,从而提高优化效果。目前已有几种常用的算法来操纵任务梯度以形成一个合适的更新向量:
- MGDA:该算法直接优化解到帕累托集,这意味着它试图找到一组参数,这些参数在所有任务上都能达到最优或接近最优的性能。
- GradNorm:使用预定义的启发式方法动态重新加权每个损失函数$L_i$。这种方法通过调整每个任务的权重来减少梯度冲突,从而提高整体性能。
- PCGrad:识别并基于冲突梯度来操纵梯度,并将每个任务梯度投影到其他任务梯度的法平面上以减少冲突。这种方法通过减少任务梯度之间的冲突来提高MTL的性能。
尽管这些方法能够提高MTL的学习性能,但它们在操纵梯度时没有考虑到原始目标$g_0$。因此上述方法理论上会收敛到帕累托集中的任何点,而不是我们指定的最优点$L_0^*$。
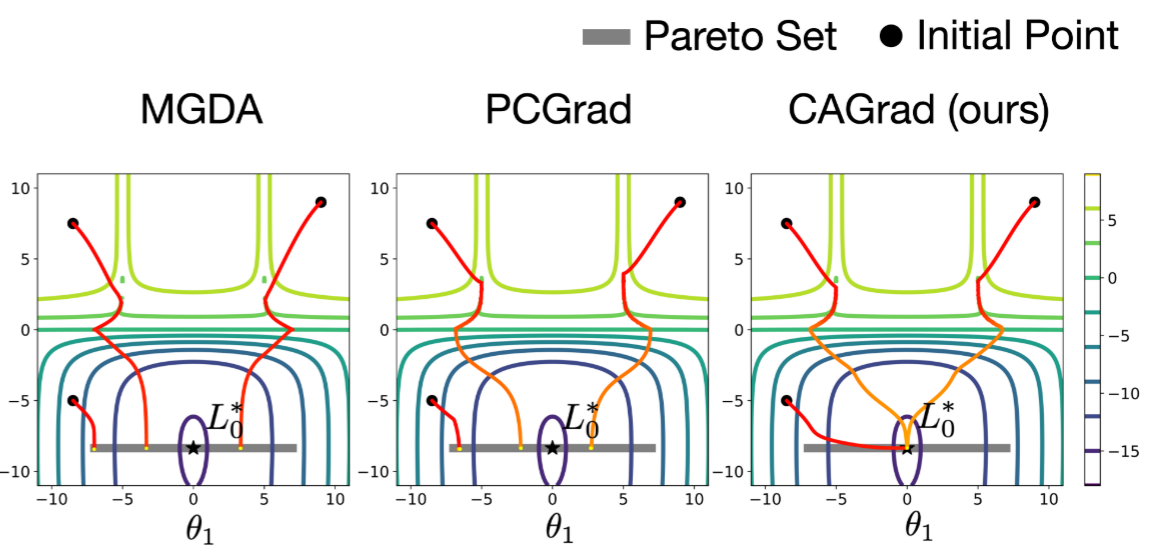
冲突规避梯度下降
对于梯度下降过程来说$\theta^\prime\rightarrow\theta-\alpha d$,其中$\alpha$代表学习率,$d$为方向向量。我们考虑下面这样一个问题:我们向找到一个更新方向$d$,不仅使任务平均损失$L_0$下降,而且会使每个任务的损失$L_i$都下降,形式化如下
$\begin{aligned}R(\theta,d)=\max_{i\in[K]}\left\{\frac{1}{\alpha}\left(L_i(\theta-\alpha d)-L_i(\theta)\right)\right\}\approx-\min_{i\in[K]}\langle g_i,d\rangle\qquad(p1)\end{aligned}$
直观来看,$R(\theta,d)$用于找到一个损失差值最大的梯度$i$,当$R(\theta,d)>0$时,说明当前更新方向$d$会使任务$i$的损失上升。如果$R(\theta,d)<0$,这意味着在更新方向$d$下,所有任务损失都随着更新而减少。这里$\langle g_i,d\rangle=\|g_i\|\|d\|\cos(g_i,d)$代表任务$i$的梯度与更新方向的内积,可以用来表示更新方向和任务梯度是否冲突,$\langle g_i,d\rangle>0$表示不冲突,因此$R(\theta,d)$也可用来衡量梯度冲突。
约等号可通过一阶泰勒展开证明
$\begin{aligned}L_i(\theta-\alpha d)\approx L_i(\theta)-\alpha\nabla L_i(\theta)^T d=L_i(\theta)-\alpha\langle g_i,d\rangle\end{aligned}$
$\begin{aligned}\frac{1}{\alpha}\left(L_i(\theta-\alpha d)-L_i(\theta)\right)\approx-\langle g_i,d\rangle\end{aligned}$
$\begin{aligned}\max_{i\in[K]}\left\{\frac{1}{\alpha}\left(L_i(\theta-\alpha d)-L_i(\theta)\right)\right\}\approx\max_{i\in[K]}\left\{-\langle g_i,d\rangle\right\}\approx-\min_{i\in[K]}\langle g_i,d\rangle\end{aligned}$
基于$R(\theta,d)$,我们期望找到一个所有任务损失都下降的方向,即$R(\theta,d)<0$,也即$\min_{i\in[K]}\langle g_i,d\rangle>0$。下面我们可以推导出CAGrad的优化目标了,即尽可能最大化梯度冲突$\min_{i\in[K]}\langle g_i,d\rangle$(即最小化$R(\theta,d)$),同时保证解收敛到主要目标$L_0^*(\theta)=g_0$,形式化如下
$\begin{aligned}&\max_{d\in\mathbb R^m}\min_{i\in[K]}\;\langle g_i,d\rangle\\&\mathrm{s.t.}\|d-g_0\|\le c\|g_0\|\end{aligned}\qquad(p2)$
这里$c\in[0,1)$是一个用于控制收敛速率的超参数。约束条件保证了更新向量$d$与平均梯度$g_0$的距离不超过$c\|g_0\|$。即在以平均梯度$g_0$为中心的局部球内寻找最佳更新向量,确保最优解收敛到$g_0$附近。
对偶问题
与前文的思路类似,由于神经网络中$d\in\mathrm R^m$的维度过高不好直接求解问题$p1$,因此我们可以从其拉格朗日对偶问题入手,将求解高维$d\in\mathrm R^m$问题转换成求解低维权重$w\in\mathrm R^K$的问题。
首先注意到
${\min}_{i}\langle g_{i},d\rangle=\min_{w\in\mathcal{W}}\langle\sum_{i}w_{i}{g_{i}},d\rangle$
其中$w=(w_{1},\ldots,w_{K})\in\mathbb{R}^{K}$,$\mathcal W$代表概率单纯形$\mathcal{W}=\{w{:}\sum_{i}w_{i}=1\mathrm\;\text{and}\;w_{i}\geq0\}$。等式证明如下
对于等式右侧由内积的线性运算性质有
$\min_{w\in\mathcal{W}}\langle\sum_{i}w_{i}{g_{i}},d\rangle=\min_{w\in\mathcal{W}}\sum_{i}w_{i}\langle{g_{i}},d\rangle$
目标函数$f(w)=\sum_{i}w_{i}\langle{g_{i}},d\rangle$。是关于$w$的线性函数,而约束集$\mathcal W$是概率单纯形(凸紧集),根据线性优化理论,线性函数在凸紧集上的极值必定出现在极点上。而对于概率单纯形来说,其极点一定在标准基向量上取到,即每个极点$e_i$对应一个确定性分布:第$i$个事件发生的概率为$1$,其余为$0$。因此,极值点对应选择单个$i$。在极点$e_i$处,目标函数值为:
$f(e_i)=\langle g_i,d\rangle$
左右两侧的最小值均通过选择使得$\langle g_i,d\rangle$最小的$i$达到,因此等式成立
${\min}_{i}\langle g_{i},d\rangle=\min_{w\in\mathcal{W}}\langle\sum_{i}w_{i}{g_{i}},d\rangle$
下面令$g_w=\sum_iw_ig_i$以及${\phi}=c^2\left\|g_0\right\|^2$,则问题$p2$的拉格朗日对偶问题如下
$\begin{aligned}&\max_{d}\min_{\lambda,w}\;g_w^\top d-\lambda(\left\|g_0-d\right\|^2-\phi)/2\\&\mathrm{s.t.}\;d\in\mathbb{R}^m,\;\lambda\geq0,w\in\mathcal{W}\end{aligned}\qquad(p3)$
这里为了便于处理$\ell_2$范数及其导数,这里将约束转换为了平方形式,并且使用$\frac{\lambda}{2}$作为拉格朗日系数
$\|g_0-d\|^2\le c^2\|g_0\|^2$
进一步的,由于$d$的目标是凸优化问题,并且等式约束是仿射函数,因此当$c>0$时满足Slater条件,原问题是一个强对偶问题。因此问题$p3$可以交换最大-最小化形式如下
$\begin{aligned}&\min_{\lambda,w}\max_{d}\;g_w^\top d-\lambda\left\|g_0-d\right\|^2/2+\lambda\phi/2\\&\mathrm{s.t.}\;d\in\mathbb{R}^m,\;\lambda\geq0,w\in\mathcal{W}\end{aligned}\qquad(p4)$
求解对偶问题
对于问题$p4$,我们首先优化其内层的最大化问题,内层的KKT条件为
$\begin{aligned} \frac{\partial L_d}{\partial d}=g_w-\lambda(d-g_0)=0 \end{aligned}$
因此固定$\lambda,w$,内层最优解为$d=g_0+\frac{g_w}{\lambda}$,带入问题$p4$可得以下对偶问题
$\begin{aligned}&\min_{\lambda,w}\;g_w^\top (g_0+\frac{g_w}{\lambda})-\frac{\lambda}{2}\left\|{g_w}/{\lambda}\right\|^2+\frac{\lambda}{2}\phi\\&\mathrm{s.t.}\;\lambda\geq0,w\in\mathcal{W}\end{aligned}\qquad(p5)$
等价于
$\begin{aligned}&\min_{\lambda,w}\;g_w^\top g_0+\frac{1}{2\lambda}\|g_w\|^2+\frac{\lambda}{2}\phi\\&\mathrm{s.t.}\;\lambda\geq0,w\in\mathcal{W}\end{aligned}\qquad(p6)$
固定$w$,则针对$\lambda$的KKT条件如下
$\begin{aligned} \frac{\partial L_\lambda}{\partial \lambda}=\frac{\phi}{2}-\frac{\|g_w\|^2}{2\lambda^2}=0 \end{aligned}$
则最优解为$\lambda=\|g_w\|/\phi^{1/2}$,带入问题$p6$可得最终的对偶问题
$\begin{aligned}&w^*=\arg\min_{w}\;g_w^\top g_0+\sqrt{\phi}\|g_w\|\\&\mathrm{s.t.}\;w\in\mathcal{W}\end{aligned}\qquad(p7)$
我们可以通过梯度下降算法或者一些优化库如cvxpy来快速求解上述的优化问题。CAGrad的算法流程如下
- 算法名称:$\textbf{CAGrad}$
- 算法输入:初始神经网络参数$\theta_0$,多任务损失函数$\{L_i\}_{i=1}^K$,收敛范围超参数$c\in[0,1)$,学习率$\alpha\in\mathbb R^+$
- 算法输出:第$t$次迭代更新后的参数$\theta_t$
- 算法流程:
- $\textbf{repeat}$
- $\quad$在第$t$次迭代中,定义收敛约束目标$g_0=\frac 1K\sum_{i=1}^K\nabla L_i(\theta_{t-1})$和$\phi=c^2\|g_0\|^2$
- $\quad$使用约束求解器求解$\min_{w\in\mathcal W}F(w):=g_w^\top g_0+\sqrt{\phi}\|g_w\|$,其中$g_w=\frac 1K\sum_{i=1}^K w_i\nabla L_i(\theta_{t-1})$
- $\quad$基于最优权重梯度组合$g_{w^*}$求最优更新方向$d^*=g_0+\frac{\sqrt\phi}{\|g_w\|}g_w$
- $\quad$使用最优更新方向更新参数$\theta_t=\theta_{t-1}-\alpha\left(g_0+\frac{\sqrt\phi}{\|g_w\|}g_w\right)$
- $\textbf{until convergence}$
代码实现
下面是CAGrad算法的三种实现
#CAGrad算法的标准实现
def cagrad(self, grad_vec, num_tasks):
"""
grad_vec: [num_tasks, dim]
"""
"""
grad_vec:一个形状为 [num_tasks, dim] 的张量,表示每个任务的梯度。num_tasks 是任务数量,dim 是参数的总维度。
num_tasks:任务的数量
"""
#[g1,g2,g3,...,gn]
grads = grad_vec
#grads.mm(grads.t()):计算梯度矩阵的协方差矩阵 GG,形状为 [num_tasks, num_tasks]
"""
GG=
[[g1g1,g1g2,...,g1gn]
[g2g1,g2g2,...,g2gn]
...
[gng1,gng2,...,gngn]]
"""
GG = grads.mm(grads.t()).cpu()
#缩放协方差矩阵
#计算协方差矩阵对角线元素的平方根的均值作为缩放因子。
#将协方差矩阵 GG 缩放,使其对角线元素的均值接近 1,以避免数值不稳定。
scale = (torch.diag(GG)+1e-4).sqrt().mean()
GG = GG / scale.pow(2)
#Gg:计算每个任务的平均梯度信息。
#gg:计算全局平均梯度信息。
"""
Gg=
[g1g0,
g2g0,
...
gng0]
(nx1)
"""
Gg = GG.mean(1, keepdims=True)
"""
gg=||g0||^2
"""
gg = Gg.mean(0, keepdims=True)
#初始化任务权重 w,形状为 [num_tasks, 1]
w = torch.zeros(num_tasks, 1, requires_grad=True)
#使用随机梯度下降(SGD)优化器,学习率根据任务数量动态调整
if num_tasks == 50:
w_opt = torch.optim.SGD([w], lr=50, momentum=0.5)
else:
w_opt = torch.optim.SGD([w], lr=25, momentum=0.5)
#计算正则化系数 c,其中 self.cagrad_c 是超参数,用于控制梯度冲突的权重
"""
c=c*||g0||
"""
c = (gg+1e-4).sqrt() * self.cagrad_c
#优化任务权重
w_best = None
obj_best = np.inf
for i in range(21):
w_opt.zero_grad()
#将权重归一化为概率分布
ww = torch.softmax(w, 0)
#任务权重与全局梯度信息的加权和
"""
优化目标obj实际上就是w*=argmin gw^T*g0+c||g0||*||gw||
"""
obj = ww.t().mm(Gg) + c * (ww.t().mm(GG).mm(ww) + 1e-4).sqrt()
#梯度下降最小化obj并求w
if obj.item() < obj_best:
obj_best = obj.item()
w_best = w.clone()
if i < 20:
obj.backward()
w_opt.step()
#正则权重w
ww = torch.softmax(w_best, 0)
#计算||gw||
gw_norm = (ww.t().mm(GG).mm(ww)+1e-4).sqrt()
#lambda=phi^{1/2}/||gw||
lmbda = c.view(-1) / (gw_norm+1e-4)
"""
g=g0+gw*λ
"""
g = ((1/num_tasks + ww * lmbda).view(
-1, 1).to(grads.device) * grads).sum(0) / (1 + self.cagrad_c**2)
return g
#CAGrad的精确实现
def cagrad_exact(self, grad_vec, num_tasks):
#将输入的梯度向量 grad_vec 归一化,除以 100。这一步是为了调整梯度的尺度,使其适合后续的优化过程
grads = grad_vec / 100.
#计算g0
g0 = grads.mean(0)
GG = grads.mm(grads.t())
#初始化权重 x_start 为均匀分布
#权重单纯形约束
x_start = np.ones(num_tasks)/num_tasks
##定义权重的边界 bnds,确保所有权重都在 [0, 1] 范围内
bnds = tuple((0,1) for x in x_start)
#定义约束 cons,确保所有权重之和为 1
cons=({'type':'eq','fun':lambda x:1-sum(x)})
"""
A=
[[g1g1,g1g2,...,g1gn]
[g2g1,g2g2,...,g2gn]
...
[gng1,gng2,...,gngn]]
"""
A = GG.cpu().numpy()
#b为初始权重矩阵
b = x_start.copy()
#计算\phi^{1/2}
c = (self.cagrad_c*g0.norm()).cpu().item()
#定义目标函数,输入为权重x
"""
优化目标obj实际上就是w*=argmin gw^T*g0+c||g0||*||gw||
"""
def objfn(x):
return (x.reshape(1,num_tasks).dot(A).dot(b.reshape(num_tasks, 1)) + \
c * np.sqrt(x.reshape(1,num_tasks).dot(A).dot(x.reshape(num_tasks,1))+1e-8)).sum()
#直接使用SciPy 的 minimize约束求解器找到最优权重 w_cpu
res = minimize(objfn, x_start, bounds=bnds, constraints=cons)
w_cpu = res.x
#将最优权重 w_cpu 转换为 PyTorch 张量 ww
ww= torch.Tensor(w_cpu).to(grad_vec.device)
#计算加权梯度 gw 和其范数 gw_norm
gw = (grads * ww.view(-1, 1)).sum(0)
#计算正则化系数 lmbda
gw_norm = gw.norm()
#计算λ
lmbda = c / (gw_norm+1e-4)
#更新参数梯度更新方向
g = (g0 + lmbda * gw) / (1 + lmbda)
#返回最终的梯度,乘以 100 以恢复原始的梯度尺度
return g * 100
#CAGrad的快速近似实现
##在 cagrad_fast 方法中,不是使用所有的任务梯度来计算协方差矩阵和进行优化,而是只随机选取一部分任务(由 self.fast_n 决定)来进行计算
def cagrad_fast(self, grad_vec, num_tasks):
#n 是快速近似方法中随机采样的任务数量
n = self.fast_n
#scale 是用于归一化梯度的因子
scale = 100.
grads = grad_vec / scale
GG = grads.mm(grads.t())
g0_norm = (self.fast_w.view(1, -1).mm(GG).mm(self.fast_w.view(-1, 1))+1e-8).sqrt().item()
#权重单纯形约束
x_start = np.ones(n) / n
bnds = tuple((0,1) for x in x_start)
cons=({'type':'eq','fun':lambda x:1-sum(x)})
A = GG.cpu().numpy()
c = self.cagrad_c*g0_norm
def objfn(x):
return (x.reshape(1,n).dot(A).dot(self.fast_w_numpy.reshape(n,1)) + \
c * np.sqrt(x.reshape(1,n).dot(A).dot(x.reshape(n,1))+1e-8)).sum()
res = minimize(objfn, x_start, bounds=bnds, constraints=cons)
w_cpu = res.x
ww= torch.Tensor(w_cpu).to(grad_vec.device)
gw = (grads * ww.view(-1, 1)).sum(0)
gw_norm = np.sqrt(w_cpu.reshape(1,n).dot(A).dot(w_cpu.reshape(n,1))+1e-8).item()
lmbda = c / (gw_norm+1e-4)
g = ((self.fast_w.view(-1,1)+ww.view(-1,1)*lmbda)*grads).sum(0)
g = g / (1 + self.cagrad_c) * scale
return g